Você sabe sobre o ajuste do ESP32 ADC ?: 29 etapas

2025 Autor: John Day | [email protected]. Última modificação: 2025-01-23 15:03

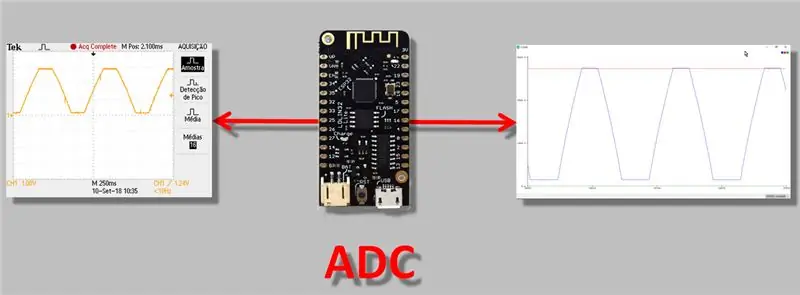
Hoje vou falar de um assunto mais técnico, mas que acho que todo mundo que trabalha com ESP32 deve saber: a questão do ADC (conversor analógico-digital) ajuste de leitura. Acho isso importante porque ao fazer uma "medição", especialmente com um instrumento que possui uma saída analógica, você precisa ter certeza absoluta de que a leitura está sendo realizada corretamente.

No vídeo de hoje, portanto, faremos medições usando o "conversor analógico-digital" do ESP32, observaremos as discrepâncias de conversão e aplicaremos um método de ajuste / calibração ADC.

Etapa 1: O que é um conversor AD?

Um conversor AD é um circuito capaz de traduzir uma quantidade analógica (contínua) em valores digitais (discretos). O que isso significa? Isso significa que enquanto os valores digitais podem assumir apenas valores discretos formados pela combinação de zeros e uns, uma grandeza analógica pode assumir qualquer valor dentro de uma faixa. Por exemplo, se medíssemos a tensão de uma célula AA ideal, poderíamos encontrar qualquer valor entre 0 V e 1,5 V, já que essa é a grandeza analógica. O estado de saída de uma lâmpada ideal deve assumir apenas dois estados (desligada ou ligada), que é uma magnitude discreta. Como os microcontroladores funcionam usando essa lógica discreta, precisamos de um circuito capaz de traduzir uma grandeza analógica em digital (ou discreta).

Etapa 2: Recursos usados

• Um cartão Lolin32 Lite v1.0.0

• Um osciloscópio Tektronix TDS1001C para captura

• Um cabo USB para o ESP32

• Um osciloscópio Hantek DSO4102C como gerador de sinal

Etapa 3: ESP32 ADC

De acordo com os dados do Espressif, os chips ESP32 podem apresentar uma diferença de +/- 6% de um chip para outro nos resultados medidos.

Além disso, a conversão NÃO tem uma resposta linear para cada faixa disponível para leitura. O Espressif fornece um método de calibração e sugere que os usuários implementem outros métodos se considerarem necessário para atingir a precisão desejada.

Faremos uma aquisição de dados e, a partir disso, mostraremos as respostas do ADC e um exemplo de aplicação de um processo matemático para leitura do ajuste.

Existem várias maneiras (mais simples ou mais complexas) de realizar essas correções. Cabe a você avaliar o mais adequado para o seu projeto.

O mostrado aqui terá um propósito ilustrativo e tentará abordar pontos interessantes que podem ser observados durante os ajustes.

Etapa 4: Circuito usado

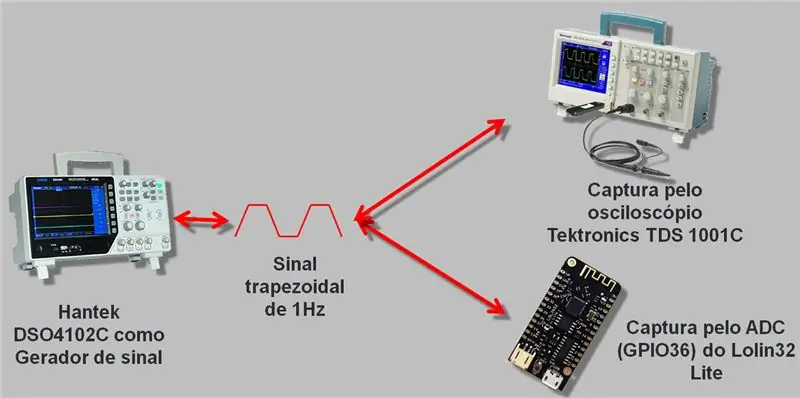
Usei um osciloscópio com gerador de sinal que vai até 25 MHz, o Hantek DSO4102C. Geramos uma onda que foi lida pelo ESP A / D e pelo osciloscópio. Os dados coletados foram registrados em csv e em planilha, que deixarei ao final do artigo para download.

Etapa 5: Sinal usado

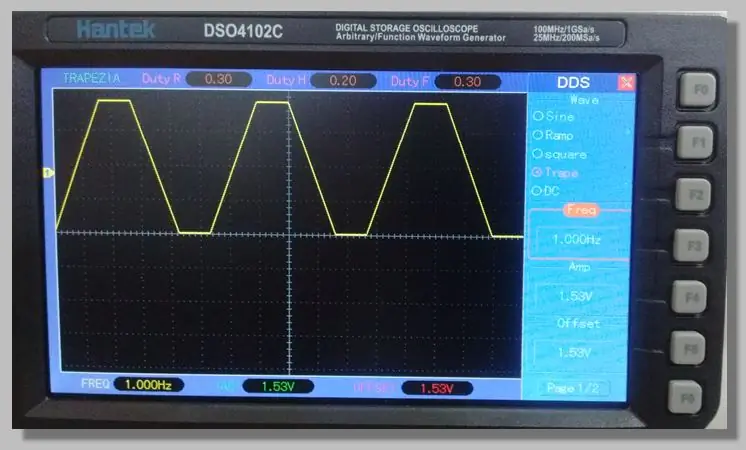
Escolhemos um sinal trapezoidal de baixa frequência que permite o acesso às rampas que percorrem toda a faixa de conversão. Isso permite um grande número de amostras nessas rampas.

Etapa 6: Dados obtidos pelo osciloscópio

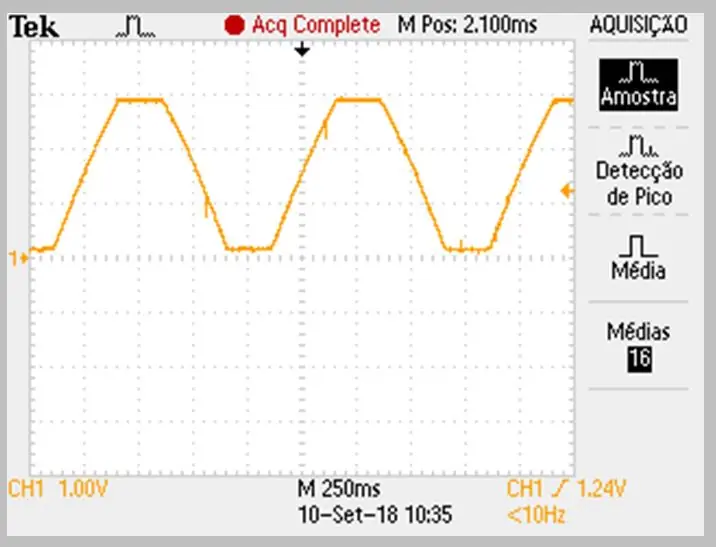
A imagem da captura foi realizada pelo osciloscópio. Os dados foram armazenados em um arquivo csv. Observe a ligeira curvatura nas rampas de subida e descida do sinal.

Etapa 7: Dados obtidos pelo osciloscópio (arquivo csv no Excel)

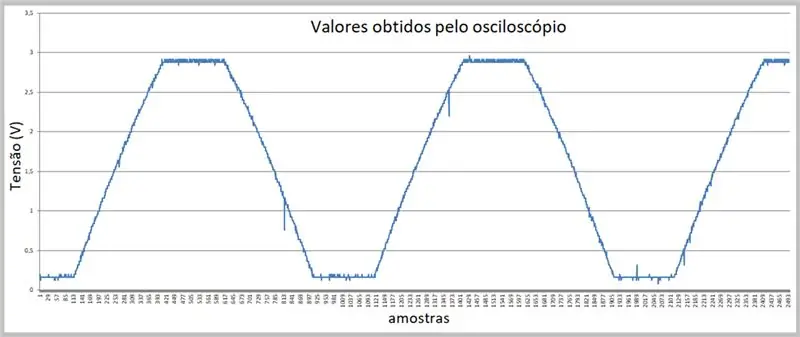
Temos as amostras aqui.

Etapa 8: Dados obtidos pelo ADC

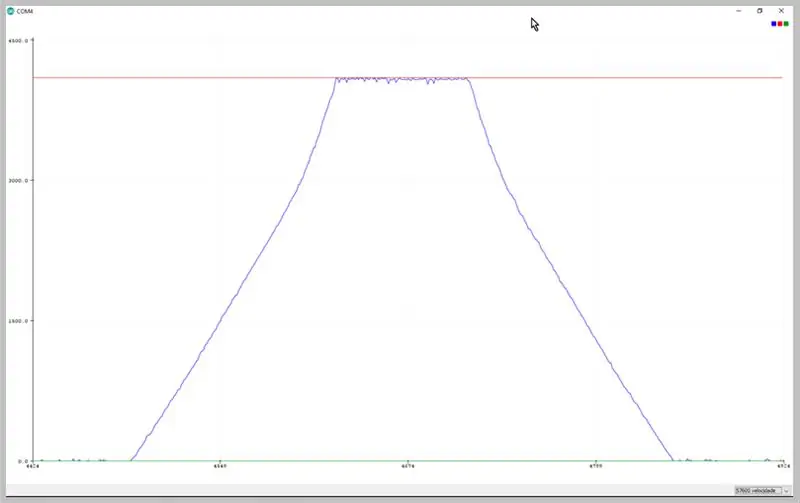
Ao alterar a taxa de transferência do serial, podemos visualizar os dados capturados pelo ADC. Observe a deformação do sinal trapezoidal.

Dados observados na plotadora serial IDE Arduino

Etapa 9: Dados obtidos por ADC - Excel

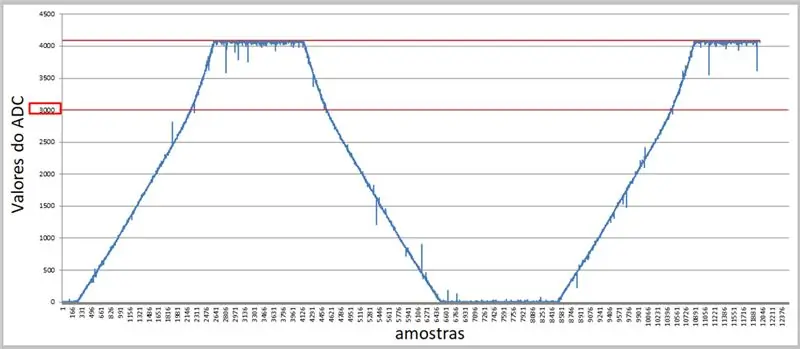
Usando uma taxa mais alta e o terminal serial, podemos capturar os valores e aplicá-los no Excel para nossas comparações.

Etapa 10: comparação das rampas de escalada

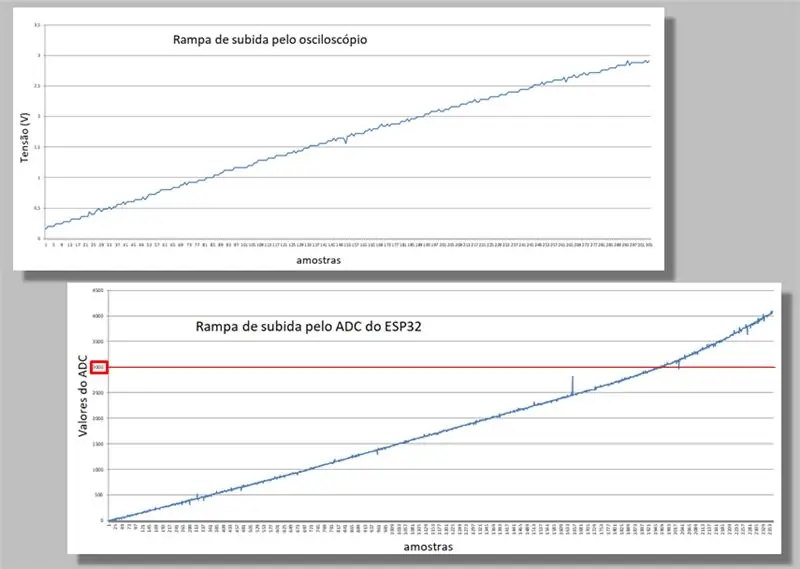
Comparamos as duas rampas de escalada das duas capturas.

Observe a curvatura que ocorre em ambas as rampas.

Observe também que, para a mesma rampa, temos muito mais amostras do ESP32 do que do osciloscópio.

Etapa 11: Equacionando o Número de Amostras

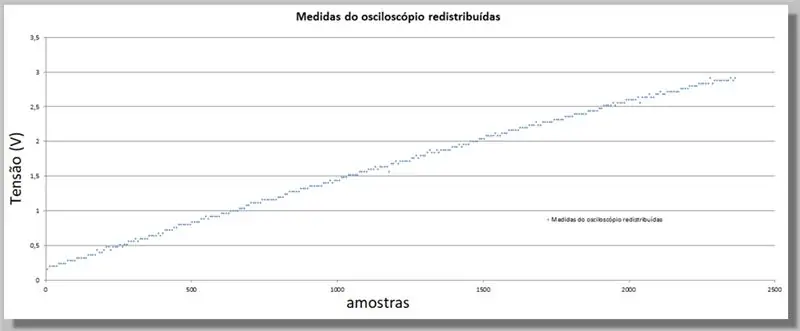
Como o ESP32 forneceu um número maior de amostras do que o osciloscópio, precisamos equacionar esses valores, pois eles servirão como um índice para comparar as duas curvas.

Para isso, faremos uma comparação direta.

Temos 305 amostras para a rampa do osciloscópio e 2365 amostras para a rampa ADC.

Como as rampas são do mesmo intervalo, podemos dizer que temos aproximadamente 7,75 amostras do ADC para cada osciloscópio.

Multiplicar o índice de cada amostra do osciloscópio tem a mesma curva, mas com índices equivalentes ao ADC e aos dados redistribuídos.

Para preencher os dados ausentes para as novas posições, aplicaremos uma curva que se ajusta estatisticamente aos dados conhecidos.

Etapa 12: Preenchendo as lacunas - Linha de tendência

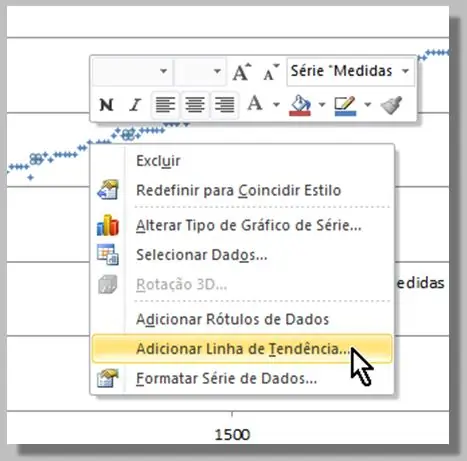
Selecionando os dados conhecidos (pontos azuis), clicando e clicando com o botão direito, selecionamos: "Adicionar linha de tendência…"

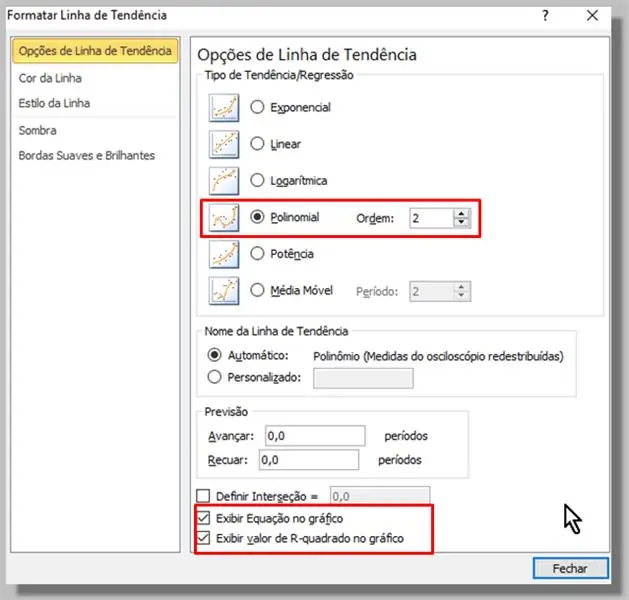
Na janela que aparece, selecionamos o tipo Polinomial (a ordem 2 será suficiente).

Também verificamos as opções "Exibir equação no gráfico" e "Exibir valor de R ao quadrado no gráfico".

Clicamos em "Fechar".

Etapa 13: Preenchendo as lacunas - Curva polinomial de grau 2

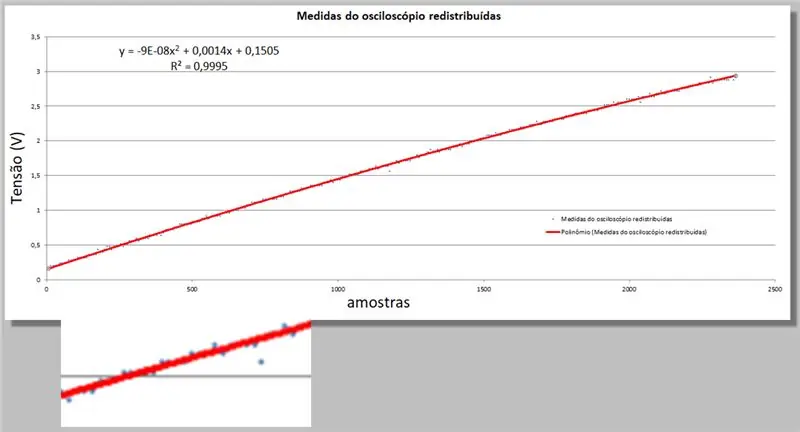
O Excel nos dá duas novas informações; a equação de segunda ordem que melhor se ajusta aos dados e a equação de R ao quadrado que quantifica essa adequação.

Lembre-se de que quanto mais próximo de 1, mais apropriada é a equação.

Não vamos nos aprofundar na matemática envolvida, vamos apenas usá-la como uma ferramenta.

Etapa 14: Preenchendo as lacunas - avaliando a função

Vamos preencher as lacunas de amostragem com os dados gerados pela equação. E então, compare-os ponto a ponto.

y = -9E-08x2 + 0, 0014x + 0, 1505

R² = 0, 9999

Tensão do osciloscópio = -9E-08 * índice 2 + 0, 0014 * índice + 0, 1505

Etapa 15: Converter a tensão do osciloscópio em um valor equivalente para comparar com o ADC

Vamos aproveitar isso para transformar também o valor da tensão do osciloscópio em um valor ADC equivalente.

Como o maior valor obtido no ADP da ESP32 foi 4095, que equivale à leitura de 2,958V para o mesmo índice, podemos afirmar que:

Cada volt nas medições do osciloscópio equivale a aproximadamente 1384,4 unidades do AD. Portanto, podemos multiplicar todas as medições do osciloscópio por este valor.

Etapa 16: Comparando as duas rampas obtidas

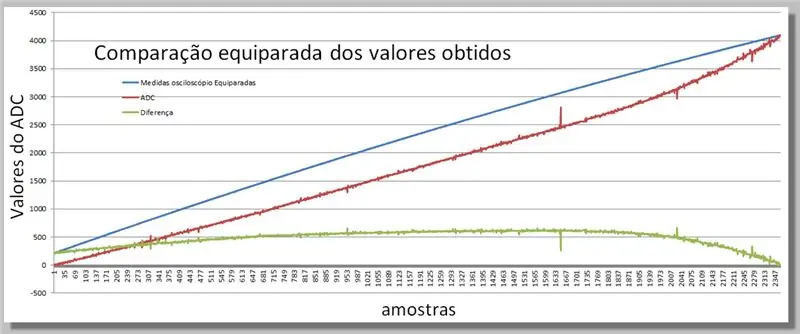
Visualizando as diferenças obtidas nas duas leituras.

Etapa 17: Comportamento da diferença de leitura ADC (ERROR)

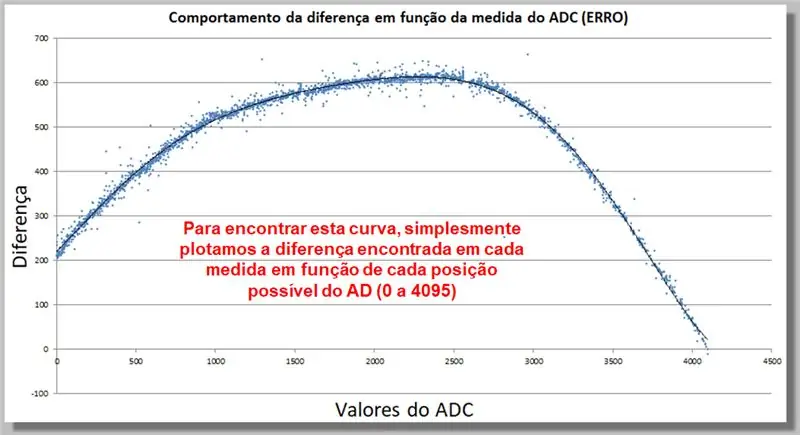
A curva abaixo mostra como a diferença na leitura do ADC se comporta em função da medição. Esta coleção de dados nos permitirá encontrar uma função de correção.

Para encontrar essa curva, simplesmente traçamos a diferença encontrada em cada medida como uma função de cada posição AD possível (0 a 4095).

Etapa 18: Comportamento de diferença de leitura do ADC - Encontrando uma função de correção

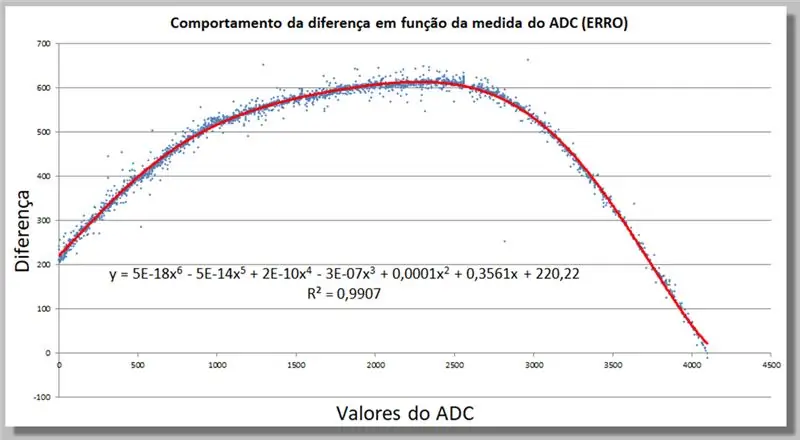
Podemos determinar no Excel uma função de correção adicionando uma Linha de Tendência, agora em um grau superior, até que se ajuste suficientemente aos nossos dados.

Etapa 19: usando outro software

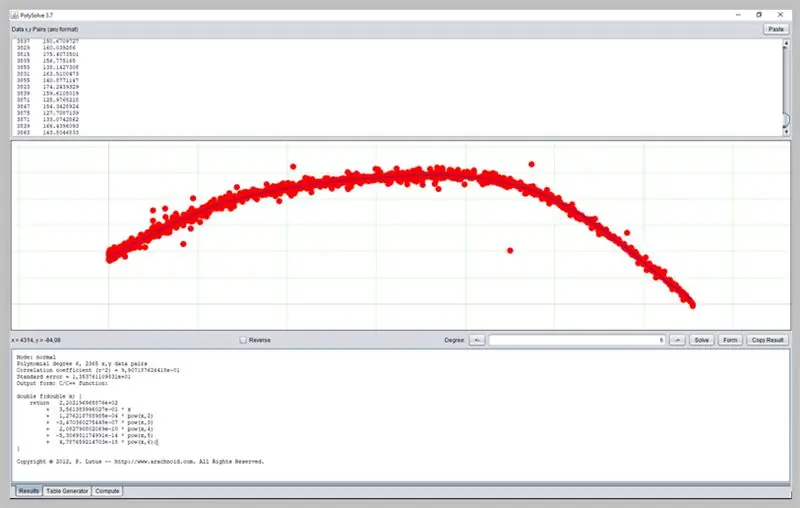
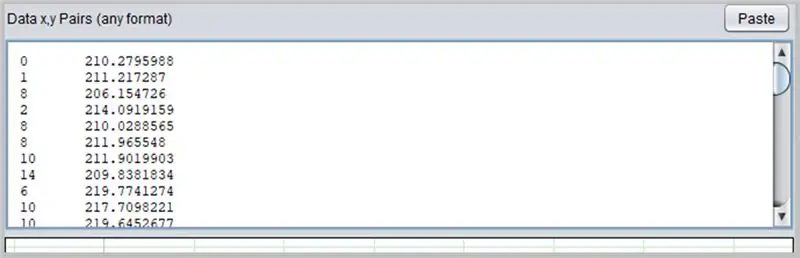
Outro software interessante para determinar curvas é o PolySolve, que pode ser usado diretamente no link: https://arachnoid.com/polysolve/ ou baixado como um aplicativo Java.

Ele permite a aplicação de regressões polinomiais de alto grau e entrega da função formatada, bem como outras funcionalidades.

Para usá-lo, basta inserir os dados na primeira caixa de texto. Os dados devem seguir a ordem X, Y separados por vírgula ou tabulação. Tenha cuidado ao usar o ponto corretamente como um ponto decimal.

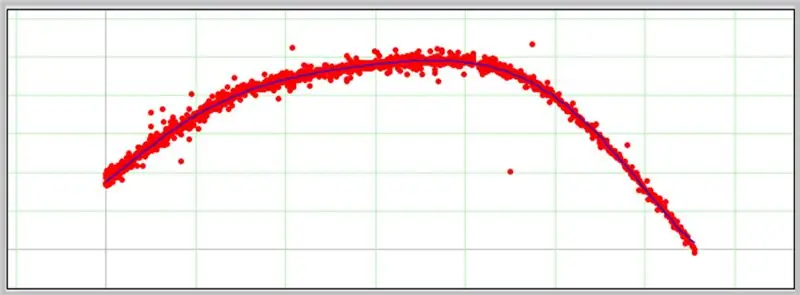
Um gráfico aparecerá na próxima caixa se os dados inseridos estiverem formatados corretamente.

Veja como foi nossa curva de erro ADC.

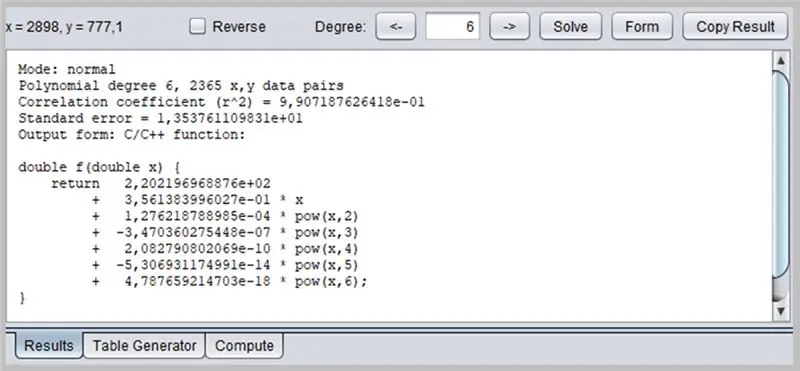
Esta janela apresentará o resultado da regressão, incluindo dados de adequação de função, que por sua vez podem ter sua saída formatada de várias maneiras: como uma função C / C ++, uma lista de coeficientes, uma função escrita em Java, etc.

Nota: Preste atenção aos separadores decimais

Etapa 20: constantes e configuração ()

Destaco aqui o GPIO usado para captura analógica. Inicializo a porta serial, bem como o pino determinado para captura analógica.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciciando uma porta serial somente para depurar pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}

Etapa 21: Loop () e a função de correção

Fazemos a captura da tensão ajustada, e imprimimos os valores com ou sem as correções corretas.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para depuração (COM CORREÇÃO) Serial.print (valor_analogico); // imprime os valores para depuração (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Observe na linha 12 que temos a opção de imprimir os dados com a adição da função diferença f (analog_value).

Etapa 22: Usar a função de correção PolySolve

Aqui, usamos a função PolySolve dentro do IDE do Arduino.

/ * Modo: grau polinomial normal 6, 2365 pares de dados x, y Coeficiente de correlação (r ^ 2) = 9, 907187626418e-01 Erro padrão = 1, 353761109831e + 01 Forma de saída: função C / C ++: Copyright © 2012, P. Lutus - https://www.arachnoid.com. Todos os direitos reservados. * / double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5,306931174991e-14 * pow (x, 5) + 4,787659214703e-18 * pow (x, 6); }

Observe a mudança de vírgula por ponto como separador decimal.

Etapa 23: Capturar com correção - Plotter Serial

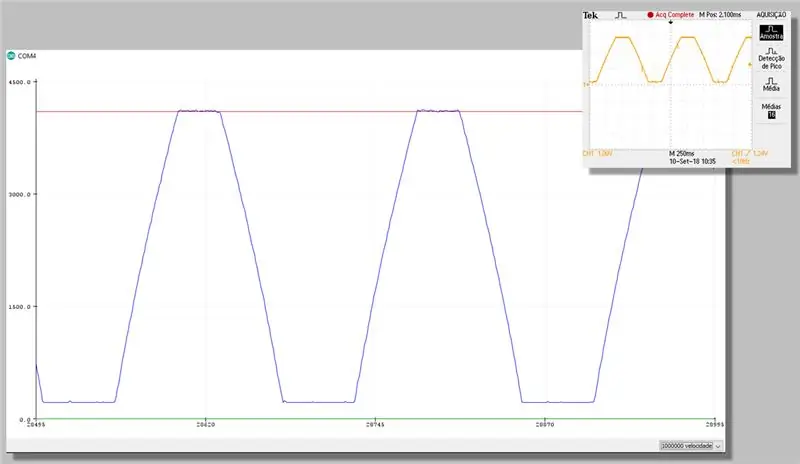
Etapa 24: Custo Computacional

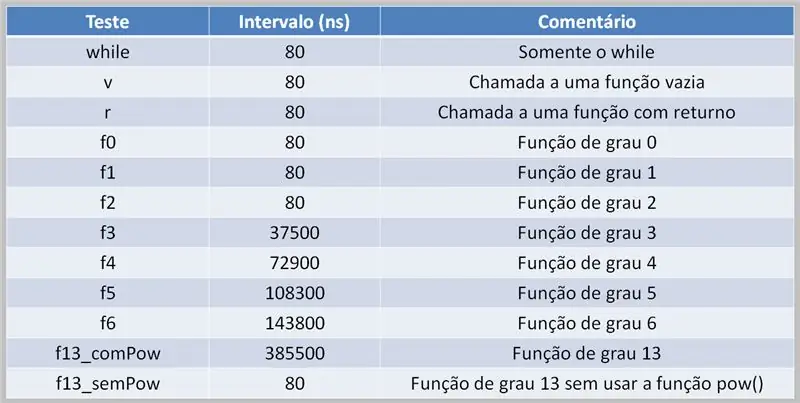
Para realizar cálculos polinomiais, é necessário que o processador realize esta tarefa. Isso pode levar a atrasos na execução, dependendo do código-fonte e da capacidade de computação disponível.

Aqui, vemos uma tabela de resultados de um teste usando polinômios de vários graus. Observe a diferença entre os momentos em que a função pow () foi usada e quando não foi.

Etapa 25: Código de teste - configuração () e início do loop ()

Aqui, temos o código usado em nosso teste.

void setup () {Serial.begin (1000000); // Iniciando um porta serial somente para depuração} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000.0; // quantidade de chamadas float contador = 0.0; // contador de chamadas

Etapa 26: Código de teste - Loop () e processamento

Usei a função micros () para obter o valor em microssegundos.

// ============= início do processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============= finaliza o processo

Etapa 27: Código de teste - Loop () - Resultados

Imprimimos o valor retornado da função de grau 13 com e sem POW para comparação, bem como o intervalo de processamento.

// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print ("-"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print ("-"); // imprime o intervalo do processamento Serial.println (agora, 6); }

Etapa 28: Código de teste - funções usadas

Funções vazias (somente com retorno) de grau 0 e 1.

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e + 02; } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }

Funções de grau 2, 3 e 4.

// FUNÇÃO DE GRAU 2duplo f2 (duplo x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * pow (x, 4); }

Funções de grau 5 e 6.

// FUNÇÃO DE GRAU 5duplo f5 (duplo x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e-10 * pow (x, 4) + -5,306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * pow (x, 4) + -5,306931174991e-14 * pow (x, 5) + 4,787659214703e-18 * pow (x, 6); }

Função de grau 13 usando o POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }

Função de grau 13 sem usar POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e-35 * x * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Etapa 29: Arquivos

Baixe os arquivos:

PDF

EU NÃO

Planilha