Detecção de tumor cerebral por ressonância magnética usando Matlab: 6 etapas

2024 Autor: John Day | [email protected]. Última modificação: 2024-01-30 11:37

Por: Madhumita Kannan, Henry Nguyen, Ashley Urrutia Avila, Mei Jin

Este código MATLAB é um programa para detectar o tamanho, formato e localização exatos de um tumor encontrado em exames de ressonância magnética do cérebro de um paciente. Este programa foi projetado para trabalhar originalmente com detecção de tumor em varreduras de ressonância magnética do cérebro, mas também pode ser usado para diagnósticos de câncer em varreduras de outros órgãos.

As instruções a seguir descreverão primeiro os métodos de análise de imagem por meio da filtragem e limpeza da varredura de ressonância magnética, por meio de binarização, filtragem de mediana e janelas deslizantes. Em seguida, ele instruirá sobre como isolar o tumor usando uma máscara elíptica pré-gerada e filtrando-a ainda mais para delinear o perímetro da forma do tumor.

Assim que o tumor for detectado, as instruções irão descrever como incorporar este programa em uma interface gráfica do usuário (GUI). Ao longo dessas instruções, o código e os arquivos apropriados serão anexados para ajudar a explicar como funciona essa análise de varredura de ressonância magnética.

Algumas coisas para saber, baixar e preparar antes de continuar com este instrutível: 1. Certifique-se de ter baixado a versão mais recente do MATLAB. Você pode instalar o R2018b aqui:

2. Para executar este programa, você precisa ter acesso aos arquivos de ressonância magnética do cérebro. Embora alguns sempre possam ser encontrados nas imagens do Google, uma análise completa e precisa pode ser realizada a partir de imagens adequadas de várias camadas de varreduras cerebrais de cada paciente. Você pode acessar os arquivos de 20 pacientes diferentes com glioblastoma pré e pós-tratamento a partir deste banco de dados:

3. O foco deste programa e os vários métodos que orientam este projeto são descritos neste documento de pesquisa:

Etapa 1: iniciar a interface gráfica do usuário (GUI)

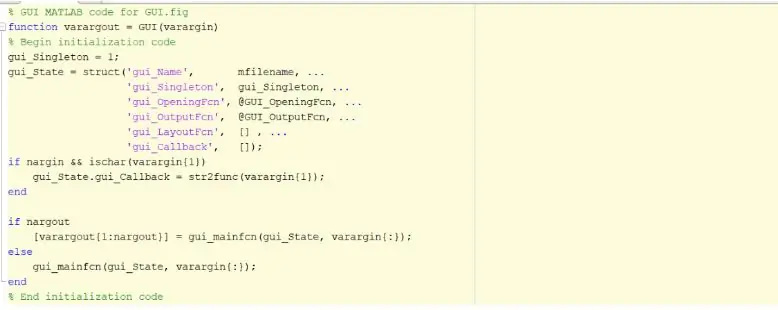
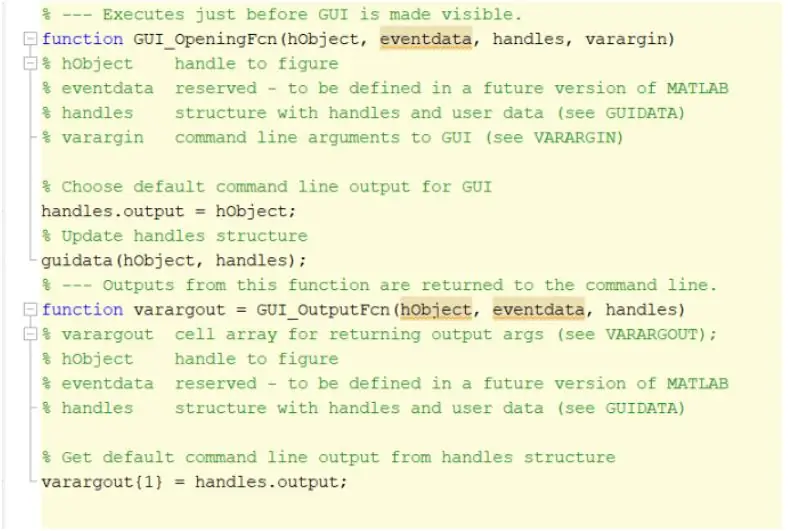
A primeira etapa seria criar e iniciar a interface gráfica do usuário, GUI. Isso pode ser feito digitando guia na janela de comando, pressionando enter e criando uma nova GUI. Depois que essa etapa for concluída, você pode começar a criar funções como eixos, texto estático, editar texto e botões de ação que serão exibidos quando o programa for executado e o usuário puder interagir. Essas funções podem ser editadas e manipuladas através do inspetor de propriedades, porém a característica mais importante que deve ser alterada na hora de criar essas funções é o nome do Tag. É importante alterar o nome do Tag de cada função implementada, pois isso nos permitirá criar uma função de retorno de chamada distinguível. Quando estiver satisfeito com o layout de sua GUI, você pode prosseguir com o carregamento dos arquivos DICOM que serão exibidos na GUI.

Etapa 2: Carregar e ler imagens de ressonância magnética no MATLAB

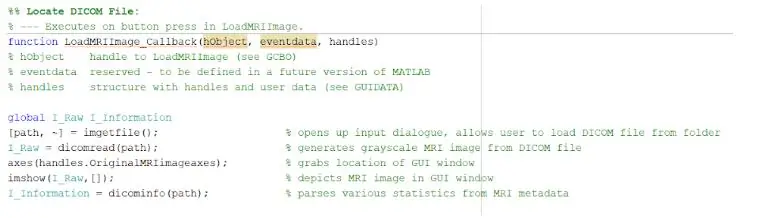
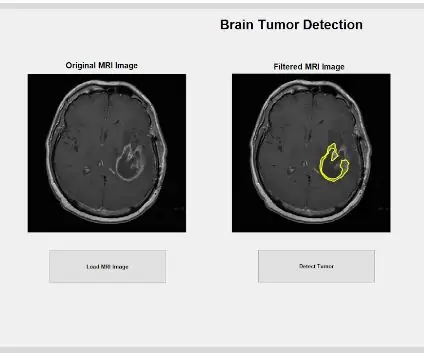
Para carregar os arquivos DICOM, você teria que inicializar corretamente a função de retorno de chamada que seria executada ao pressionar o botão “Carregar imagem de ressonância magnética”. Depois de concluído, você deve criar uma variável global que exibiria a imagem nos eixos das alças onde deseja que a imagem de ressonância magnética original seja exibida. As imagens de varredura de ressonância magnética baixadas do banco de dados são todos arquivos formatados em DICOM que precisam ser carregados no diretório MATLAB. Localize o arquivo usando imgetfile para carregá-lo no programa. As imagens são lidas usando a função embutida do MATLAB ‘dicomread’, e a primeira imagem bruta de cada arquivo é embutida nos eixos da GUI à esquerda usando imshow.

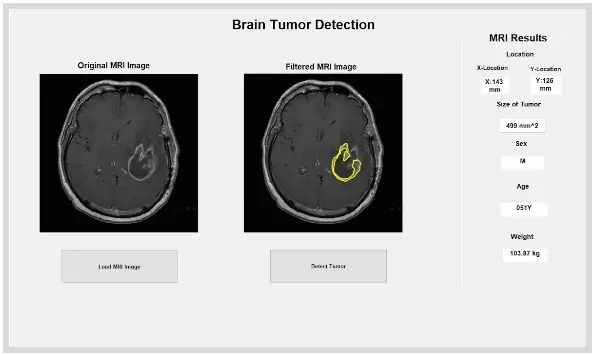
A função integrada do MATLAB ‘dicominfo’ também é extremamente útil para abordar todas as informações de cada arquivo dicom de ressonância magnética. Utilizamos essa função para extrair todas as informações descritivas dos pacientes, como sexo, idade, peso e altura. Essa função também fornece a ordem da pilha, que é útil para a implementação do programa na interface gráfica do usuário. Criamos variáveis para cada uma das informações descritivas dos pacientes que serão utilizadas para a GUI quando o botão de detecção for pressionado.

Etapa 3: Filtragem de imagens

Uma vez que o arquivo DICOM da imagem bruta foi carregado e lido, a imagem precisa ser convertida de tons de cinza em uma forma binarizada consistindo apenas de pixels em preto e branco. Usamos a função 'imbinarizar' para criar uma imagem binária a partir da imagem bruta por controlar aspectos de limiar adaptativo com valor de sensibilidade de 0,59. O fator de sensibilidade de limite padrão, 0,5, era baixo e não era capaz de detectar manchas e manchas mais brilhantes da imagem, então o aumentamos para 0,59.

A imagem binarizada é então processada por meio de um filtro de mediana usando a função ‘medfilt2’ porque a imagem binarizada é bidimensional. Definimos cada pixel de saída para conter o valor médio na vizinhança 5 x 5 em torno do pixel correspondente na imagem binarizada de entrada. Isso reduz o ruído e preserva as bordas em um quadrado 5 x 5 ao redor de cada pixel. Em seguida, aplicamos uma janela deslizante usando 'strel', para criar um elemento de estruturação plano em forma de disco com um raio de vizinhança de 2 para identificar cada pixel central de origem, em cada vizinhança do disco. Utilizamos um elemento de estruturação de disco porque estamos analisando cada ponto circular e os pixels dentro de cada ponto, portanto, um elemento em forma de disco é mais útil.

Uma vez que a imagem foi filtrada, ela pode ser limpa usando a função 'imclose' para remover os pontos pretos entre os pixels brancos filtrados na imagem e fechar todas as lacunas ao seu redor. A imagem completamente processada pode então ser plotada na segunda subparcela da figura pré-alocada, permitindo uma comparação entre a imagem bruta e a imagem filtrada.

Etapa 4: Isolamento do tumor através da máscara elíptica

Os pontos brilhantes do tumor podem então ser isolados da imagem filtrada principal através de uma máscara elíptica pré-gerada. Para criar esta máscara, você deve saber o tamanho da imagem original de ressonância magnética bruta e, usando seu comprimento de linha e coluna, como coordenadas xey, respectivamente, alocar as coordenadas centrais para a elíptica. Definimos o eixo y como um eixo principal com um raio de 50 unidades do centro e o eixo menor com um raio de 40 unidades do centro.

Usamos a função MATLAB 'meshgrid' para gerar um plano cartesiano com coordenadas bidimensionais de grade com base nas coordenadas contidas em vetores de 1 ao comprimento do eixo x, e de 1 ao comprimento do eixo y da imagem. Col é uma matriz onde cada linha é uma cópia do eixo xe Row é uma matriz onde cada coluna é uma cópia do eixo y. A grade cartesiana representada pelas coordenadas Col e Row tem comprimento (1: Y_Size) linhas e comprimento (1: X_Size) colunas. Use os índices de Col e Row gerados pela grade cartesiana para determinar a equação da elipse dependendo do raio predeterminado e das coordenadas centrais. O contorno elíptico agora pode ser preenchido com os pixels brancos encontrados nas manchas tumorais.

Utilizando a máscara elíptica pré-gerada, podemos cortar o tumor específico que você deseja analisar a partir da imagem filtrada. A máscara elíptica detecta quais pontos se encaixam logicamente no contorno da elipse e aceita isso como um ponto na imagem filtrada para ser aceitável como um tumor. A função ‘bwareafilt’ então filtra todos os outros objetos fora deste tumor detectado da imagem. Usamos uma janela específica de 500 por 4000 empiricamente com base nas dimensões de todas as imagens. Em seguida, aplicamos outra janela deslizante com "strel" como um elemento estruturante em forma de disco plano de um raio de vizinhança maior de 6, para fechar as lacunas entre cada pixel branco central dentro do tumor detectado. O local do tumor detectado é ainda mais limpo usando "imclose" para eliminar ainda mais os pixels pretos e preencher todos os orifícios com "imfill". Este tumor processado pode então ser exibido no terceiro subplot no gráfico pré-alocado para fornecer uma comparação entre o tumor isolado e as imagens originais e filtradas da varredura de ressonância magnética.

Etapa 5: delineamento do tumor

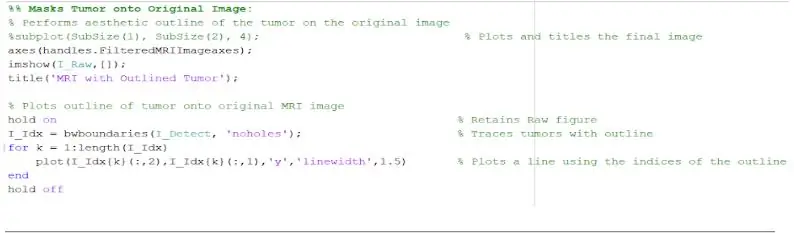
Agora que o tumor está isolado com a máscara, ele pode ser contornado e exibido na imagem original, para mostrar sua localização exata. Para fazer isso, usamos a função ‘bwboundaries’ para traçar o tumor previamente detectado com um contorno. Especificamos o contorno para não incluir os orifícios dentro do objeto de tumor conforme ele está sendo delineado. Isso pode ser plotado na imagem original, em bruto, usando um loop 'for' que traça o contorno ao redor do tumor usando os índices da linha com uma largura de linha de 1,5 pixels. Este contorno é então plotado na imagem bruta, mostrando o tamanho e localização exatos do tumor, em relação à ressonância magnética original.

Etapa 6: Analisando as propriedades físicas dos tumores

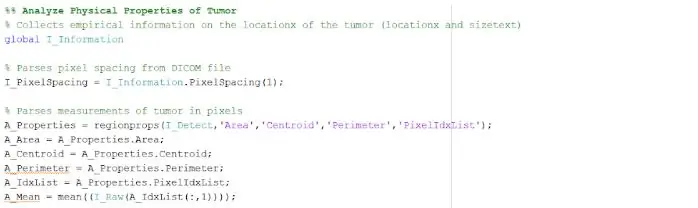
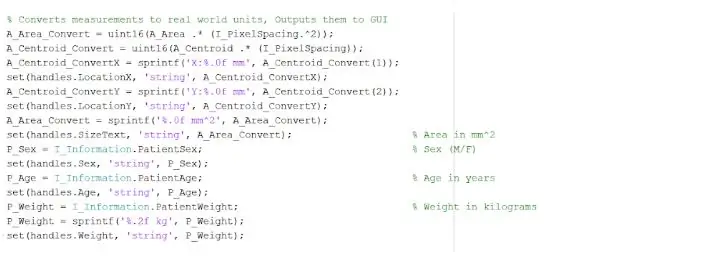
O local isolado e delineado pode nos fornecer informações úteis sobre o tamanho, área e localização do tumor. Usamos a função ‘regionprops’ para detectar as propriedades do tumor que pertencem à área, perímetro, centroides e o valor do índice de pixel. Este valor de índice de pixel nos dá as unidades do mundo real para cada pixel de cada imagem, exclusivas para cada varredura. Essas propriedades podem então ser convertidas em unidades de milímetros do mundo real. A informação empírica que o programa nos fornece é única para cada exame de ressonância magnética e é extremamente útil para determinar o tamanho, localização e tipo de tumor, que os usuários podem analisar e incorporar na interface gráfica do usuário.