Eyeballing Your Eyeball's Prescription: a BME60B Project: 9 Steps

2024 Autor: John Day | [email protected]. Última modificação: 2024-01-30 11:35

Por: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste

A ampliação é uma das principais características dos óculos de leitura, que são classificados pela prescrição de dioptrias. De acordo com a Michigan Technology University, uma dioptria é uma distância focal da lente, geralmente medida em mm, na unidade de metros (Michigan Technology University). Como os óculos de leitura têm lentes convexas, a distância focal seria positiva, fazendo com que as dioptrias também fossem positivas (Hiperfísica). A distância focal aumenta à medida que a distância entre o objeto se afasta da lente real, e isso faz com que as dioptrias diminuam, pois são inversamente proporcionais. Portanto, ter óculos de leitura com dioptrias adicionais ajudaria a lente a ampliar a visualização, de modo que possa parecer que a distância focal é menor, aumentando o valor das dioptrias.

O código apresentado será usado para prever a dioptria de uma lente com uma prescrição desconhecida. Duas entradas são usadas para calcular a prescrição: uma fotografia do fundo controlado sem o uso de lentes e outra fotografia do mesmo fundo, mas através da lente de escolha. O programa medirá a distorção entre essas duas fotografias. A partir daí, seremos capazes de estimar a dioptria da lente e produzir um resultado para o usuário visualizar.

Para este Instructable, você precisará de:

• Um padrão quadriculado em preto e branco impresso em uma folha de papel 11x8,5
• Uma câmera com a capacidade de travar seu foco
• Um tripé ou algo semelhante para proteger a câmera
• Várias prescrições de óculos de leitura
• MATLAB

Etapa 1: tirar fotos

Para calcular a ampliação de uma lente, você precisa ser capaz de compará-la com o tamanho real do objeto. Para este projeto, estaremos comparando uma imagem ampliada a uma imagem de controle.

Assim, o primeiro passo é tirar duas fotos da mesma imagem - a primeira apenas com a câmera e a segunda com as lentes dos óculos de leitura que você deseja testar.

Você tirará uma foto de um tabuleiro de xadrez preto e branco de 8,5 x 11 pol. Com uma grade de 1 pol. Configure sua câmera 11in de distância do tabuleiro de damas. Antes de tirar as fotos, trave o foco no tabuleiro de damas.

Tire uma foto do tabuleiro de damas sem os óculos de leitura. Em seguida, sem mover nada, coloque os óculos de leitura na frente da câmera e tire a segunda foto.

Certifique-se de que a posição da câmera não se mova entre as fotos. A única coisa que deve mudar entre as duas fotos é a presença das lentes dos óculos na frente da câmera.

Quando terminar de usar as fotos, envie-as para o seu computador.

Etapa 2: Carregar as imagens no MATLAB

Abra um novo script.

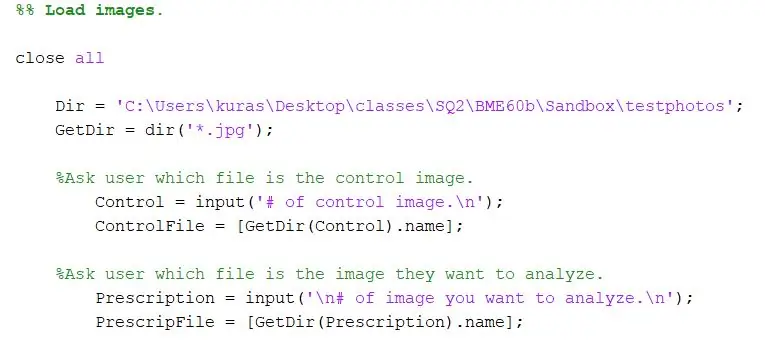
Primeiro, especifique o diretório onde as fotos são armazenadas. Em seguida, use a função dir para extrair imagens-j.webp

Dir = 'C: / Usuários / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');

Para o nosso projeto, queríamos perguntar ao usuário do programa quais arquivos eles desejavam comparar. A primeira seção pede ao usuário para especificar a imagem de controle, e a segunda pede ao usuário para especificar a imagem de teste.

• % Pergunte ao usuário qual arquivo é a imagem de controle.
• Control = input ('# da imagem de controle. / N');
• ControlFile = [GetDir (Control).name]
• % Pergunte ao usuário qual arquivo é a imagem que ele deseja analisar.
• ChooseFile = input ('\ n # da imagem que você deseja analisar. / N');
• PrescripFile = [GetDir (ChooseFile).name];

Etapa 3: Análise de imagem

Uma imagem colorida no MATLAB tem o tamanho MxNx3, enquanto uma imagem em tons de cinza tem o tamanho MxN. Isso significa que é mais rápido aprimorar / editar uma imagem em tons de cinza porque há menos dados para controlar. Use rgb2gray para converter a imagem em tons de cinza. (A função imrotate foi usada porque nossas fotos vieram na horizontal - esta linha de código pode ou não ser necessária em sua versão.)

• % converter para escala de cinza e girar
• I = imread (ControlFile);
• I = rgb2gray (I);
• I = imrotado (I, 90);

A seguir, exiba a imagem. A função subplot é usada para que a imagem de teste possa estar próxima ao controle em etapas posteriores.

• %exibição
• figura 1);
• subtrama (1, 2, 1)
• imshow (I);
• título (ControlFile);

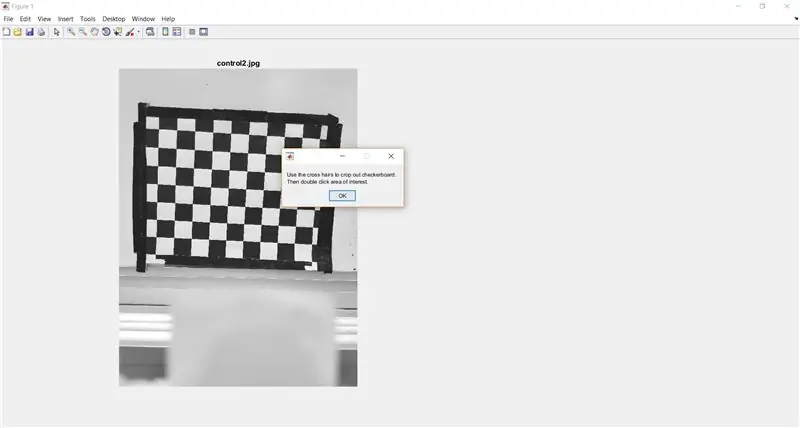
Use imcrop para solicitar ao usuário que recorte o tabuleiro de xadrez da imagem inteira. O código a seguir também mostra uma caixa de mensagem para fornecer instruções ao usuário.

• % crop out checkerboard para análise
• waitfor (msgbox ({'Use a mira para recortar o tabuleiro de xadrez.', 'Em seguida, clique duas vezes na área de interesse.'}));
• I_crop = imcrop (I);

Use imbinarize para binarizar a imagem.

I_binary = imbinarize (I_crop);

Etapa 4: calcule a largura dos quadrados brancos no tabuleiro de damas

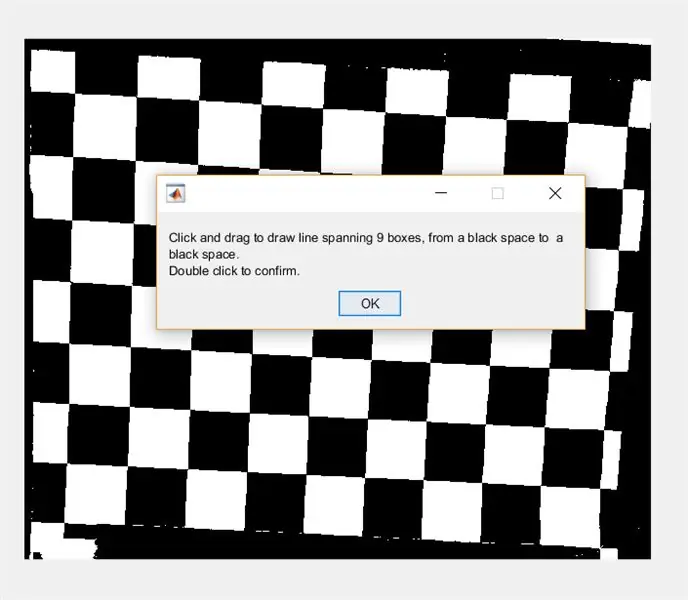
Em seguida, peça ao usuário para desenhar uma linha na imagem usando imline. Esta linha deve passar horizontalmente pelo tabuleiro de damas. Deve começar e terminar em um quadrado preto (não importa onde) - isso porque estaremos medindo a largura dos quadrados brancos, não dos pretos.

• %desenhar linha
• figura 1)
• subtrama (1, 2, 1)
• imshow (I_binary);
• waitfor (msgbox ({'Clique e arraste para desenhar uma linha que abrange 9 caixas, de um espaço preto para um espaço preto.', 'Clique duas vezes para confirmar.'}));
• linha = imline;
• posição = espera (linha);
• endpoints = line.getPosition;

Extraia os coodinates X e Y para os pontos finais da linha desenhada.

• X = pontos finais (:, 1)
• Y = pontos finais (:, 2);

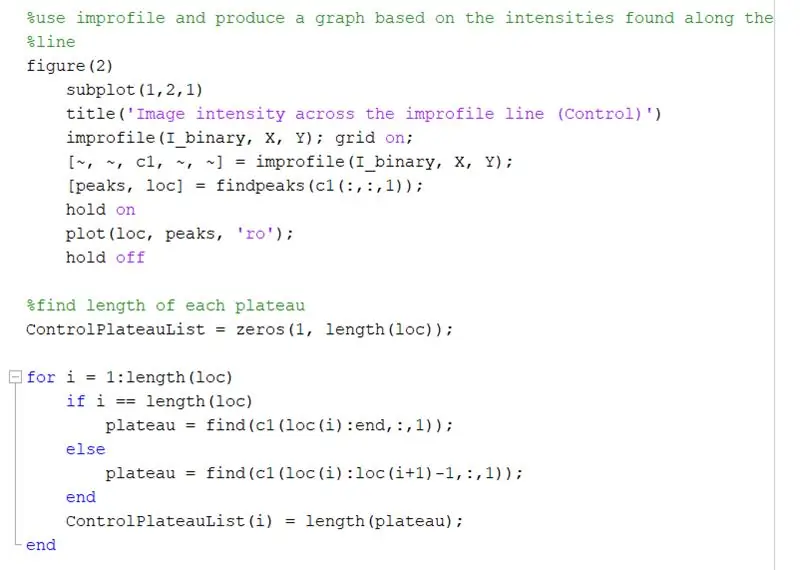
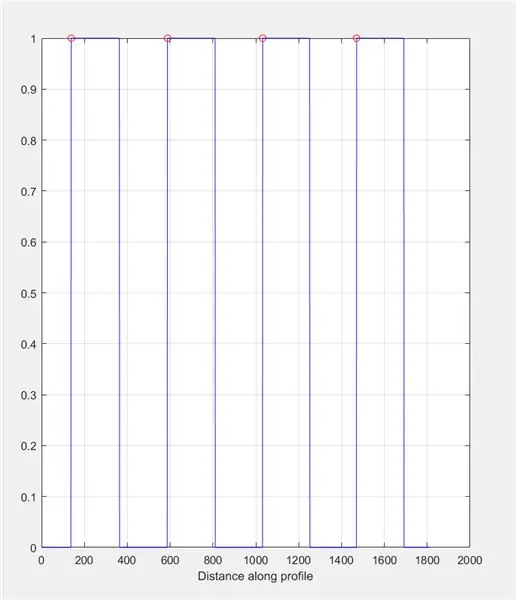
Use improfile para produzir um gráfico com base nas intensidades encontradas ao longo da linha desenhada. Deve ser semelhante a uma onda quadrada variando de 0 (preto) a 1 (branco). Calcule os picos e suas localizações também.

• Figura 2)
• subtrama (1, 2, 1)
• título ('Intensidade da imagem ao longo da linha do improfile (Controle)')
• improfile (I_binary, X, Y); grade ligada;
• [~, ~, c1, ~, ~] = improfile (I_binary, X, Y);
• [picos, loc] = encontrar picos (c1 (:,:, 1));
• aguentar
• plot (loc, peaks, 'ro');
• espere

Encontre o comprimento de cada platô no gráfico de improfile usando um loop for. Execute o loop for para a mesma quantidade de picos do gráfico do improfile. Para calcular o comprimento de cada platô, use a função ‘encontrar’ para encontrar todos os locais onde há um valor de intensidade ‘1’ em vez de ‘0’. Em seguida, calcule o comprimento dessa matriz para obter o comprimento total do platô, que deve ser igual à largura de um quadrado branco em pixels. ControlPlateauList = zeros (1, length (loc));

para i = 1: comprimento (loc)

se i == comprimento (loc)

platô = encontrar (c1 (loc (i): fim,:, 1));

outro

platô = encontrar (c1 (loc (i): loc (i + 1) -1,:, 1));

fim

ControlPlateauList (i) = comprimento (platô);

fim

Etapa 5: Repita as etapas 3 e 4 para a imagem de teste

* Nota: ao desenhar a linha improfile na imagem de teste, certifique-se de desenhá-la através dos quadrados que correspondem à linha que você desenhou na imagem de controle.

Etapa 6: Calcule a ampliação da lente

As medidas ampliadas são calculadas dividindo a média do comprimento do platô, que foi calculado no passo 5, pela média do comprimento do platô de controle, que foi calculado no passo 4. Este é calculado em 1,0884.

ampliação = média (plateauList) / média (ControlPlateauList);

Etapa 7: Encontrando R-quadrado e a prescrição do usuário por interpolação

Usando o código:

• md1 = fitlm (DadaPrescrição, MagArray);
• Rsquared = md1. Rsquared. Ordinary;

Podemos encontrar o valor R-quadrado do gráfico GivenPresciption (nossos valores dados de lentes) vs. MagArray (uma matriz das taxas de medidas de ampliação que calculamos anteriormente). Por ter um valor de R quadrado alto o suficiente, pode-se inferir que existe uma correlação forte o suficiente para justificar o uso desse método. Para este caso específico, o valor de R-quadrado foi de 0,9912, o que sugere uma forte correlação e, portanto, justifica-se o uso desse método na análise.

Usando a função:

Prescrição = interp1 (MagArray, GivenPrescription, ampliação, 'linear');

Podemos interpolar o valor de prescrição correspondente (no eixo x) de nossa taxa de ampliação (um valor no eixo y) e descobrir qual é a prescrição do usuário.

A interpolação de dados é importante para que esse método funcione, pois nos permite fazer suposições sobre as informações que não temos, com base nas informações que temos. Embora uma linha de melhor ajuste seja tecnicamente uma candidata mais forte para essa suposição, a criação de limites para reduzir o número de saídas tem o mesmo efeito que os óculos graduados vêm em valores uniformes incrementais de qualquer maneira. Isso é explicado nas etapas posteriores.

Etapa 8: Mostrar a prescrição do usuário em um gráfico

Usando o seguinte código:

• figura;
• plot (GivenPrescription, MagArray, '-g')
• aguentar
• plot (prescrição, ampliação, 'bp')
• espere
• rede
• legenda ('Dados', 'Pontos interpolados', 'Localização', 'NW')

Podemos traçar um gráfico que mostra as taxas de ampliação versus a prescrição dada com uma linha verde e os dados encontrados de nossa ampliação calculada versus nossa prescrição interpolada com uma estrela azul. Em seguida, a legenda identifica o título, o eixo x e o eixo y e coloca a legenda no canto superior esquerdo.

Etapa 9: Limite sua receita

O código a seguir é usado para produzir o arredondamento para a prescrição:

• se Prescrição <= 1,125

  CalculatedPrescription = '1.0';

• elseif Prescrição <= 1,375

  CalculatedPrescription = '1,25';

• elseif Prescrição <= 1.625

  CalculatedPrescription = '1,5';

• elseif Prescrição <= 1.875

  CalculatedPrescription = '1,75';

• elseif Prescrição <= 2,25

  CalculatedPrescription = '2.0';

• elseif Prescrição <= 2.625

  CalculatedPrescription = '2,5';

• elseif Prescrição <= 3

  CalculatedPrescription = '2.75';

• elseif Prescrição <= 3,375

  CalculatedPrescription = '3,25';

• outro

  CalculatedPrescription = 'desconhecido';

• fim

A prescrição encontrada por interpolação não reflete necessariamente a prescrição real - isso porque sempre haverá pequenas variações na análise da foto devido a erro humano. Portanto, precisamos desta etapa para classificar a prescrição real.

As prescrições que são dadas geralmente começam com 1,0 dioptria e aumentam em 0,25 em suas prescrições, portanto, após calcular a prescrição, queremos determinar a prescrição que melhor se adapta às necessidades do usuário. Depois de calcular a prescrição, executamos as declarações If fornecidas para verificar seu valor e determinar qual prescrição é necessária. Qualquer coisa menor ou igual a 1,125, então a prescrição é 1,0. Qualquer coisa menor ou igual a 1,375, a prescrição é 1,25. Qualquer coisa menor ou igual a 1,625, a prescrição é 1,5. Qualquer coisa menor ou igual a 1,845, a prescrição é 1,75. E assim por diante.

Temos os valores aumentando, pois estamos verificando se os valores são menores que. Se fizéssemos os valores diminuindo, a primeira instrução if leria a primeira instrução if o tempo todo. Se a prescrição for o menor, queremos que ele o reconheça como o menor imediatamente, então é por isso que o menor valor é o que começamos. Qualquer coisa maior do que o valor mais alto significa que a prescrição não está de acordo com nossos dados, portanto, apresentará a leitura de string “Desconhecida”.