Simulação do sistema solar: 4 etapas

2025 Autor: John Day | [email protected]. Última modificação: 2025-01-23 15:03

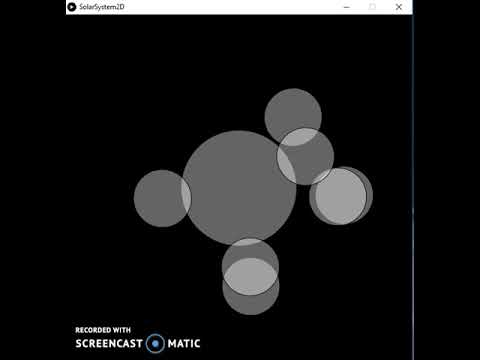
Para este projeto, eu me propus a criar uma simulação de como a gravidade afeta o movimento dos corpos planetários em um sistema solar. No vídeo acima \, o corpo do Sol é representado pela esfera de malha de arame e os planetas são gerados aleatoriamente.

O movimento dos planetas é baseado na física real, a Lei da Gravitação Universal. Esta lei define a força gravitacional exercida sobre uma massa por outra massa; neste caso, o Sol em todos os planetas e os planetas uns nos outros.

Para este projeto, usei o Processing, um ambiente de programação baseado em java. Também usei o arquivo de exemplo de processamento que simula a gravidade dos planetas. Tudo que você precisa para isso é o software de processamento e um computador.

Etapa 1: Simulação bidimensional

Comecei assistindo a alguns vídeos sobre como codificar isso que Dan Shiffman criou em seu canal no YouTube, o Trem de Codificação (Parte 1/3). Nesse ponto, pensei que usaria a recursão para gerar o sistema solar, semelhante a como Shiffman faz apenas usando as leis da física.

Eu criei um objeto planeta que tinha 'planetas filhos', que por sua vez também tinham planetas 'filhos'. O código para a simulação 2D não foi concluído porque eu não tinha uma ótima maneira de simular as forças gravitacionais para cada planeta. Eu girei a partir dessa maneira de pensar, em uma direção baseada no exemplo de processamento embutido da atração gravitacional. O problema era que eu precisava calcular a força gravitacional de todos os outros planetas em cada planeta, mas não conseguia pensar em como extrair facilmente as informações de um planeta individual. Depois de ver como o tutorial de processamento faz isso, percebi exatamente como fazer isso usando loops e arrays em vez disso

Etapa 2: levando para três dimensões

Usando o código de exemplo para Atração Planetária que vem com o processamento, iniciei um novo programa para uma simulação 3D. A principal diferença está na classe Planeta, onde adicionei uma função de atração, que calcula a força gravitacional entre dois planetas. Isso me permitiu simular como nossos sistemas solares funcionam, onde os planetas não são apenas atraídos pelo sol, mas também por todos os outros planetas.

Cada planeta tem características geradas aleatoriamente como massa, raio, velocidade orbital inicial, etc. Os planetas são esferas sólidas e o Sol é uma esfera de malha de arame. Além disso, a localização da câmera gira em torno do centro da janela.

Etapa 3: usando planetas reais

Depois de baixar a estrutura da simulação 3D, usei a Wikipedia para encontrar os dados planetários reais do nosso sistema solar. Eu criei uma série de objetos planetários e coloquei os dados reais. Quando fiz isso, tive que reduzir todas as características. Quando fiz isso, deveria ter pegado os valores reais e multiplicado por um fator para diminuir os valores, em vez disso, fiz em unidades de Terras. Ou seja, eu tomei a relação entre o valor da Terra e o valor de outros objetos, por exemplo, o Sol tem 109 vezes mais massa que a Terra. No entanto, isso resultou nos tamanhos dos planetas parecendo muito grandes ou muito pequenos.

Etapa 4: reflexões finais e comentários

Se eu continuasse trabalhando nesta simulação, refinaria / aprimoraria algumas coisas:

1. Primeiro, eu escalaria tudo uniformemente usando o mesmo fator de escala. Então, para melhorar a visibilidade das órbitas, eu adicionaria uma trilha atrás de cada planeta para ver como cada revolução se compara à anterior

2. A câmera não é interativa, o que significa que parte das órbitas estão fora da tela, "atrás da pessoa" visualizando. Há uma biblioteca de câmeras 3D chamada Peazy Cam, que é usada na Parte 2 da série de vídeos do Coding Train sobre esse tópico. Essa biblioteca permite que o visualizador gire, faça panorâmica e amplie a câmera para que seja capaz de seguir toda a órbita de um planeta.

3. Finalmente, os planetas são indistinguíveis uns dos outros. Eu gostaria de adicionar 'peles' a cada planeta e ao Sol, para que os visualizadores possam reconhecer a Terra e tal.