Cálculo Del Área Bajo La Curva De Una Función Con Python: 8 Passos

2024 Autor: John Day | [email protected]. Última modificação: 2024-01-30 11:36

Antes que nada, para desarrollar este programa debes instalar la plataforma Python desde sua página oficial:. Mais recomendable es instalar la versión 2.7.12 de 64 bits.

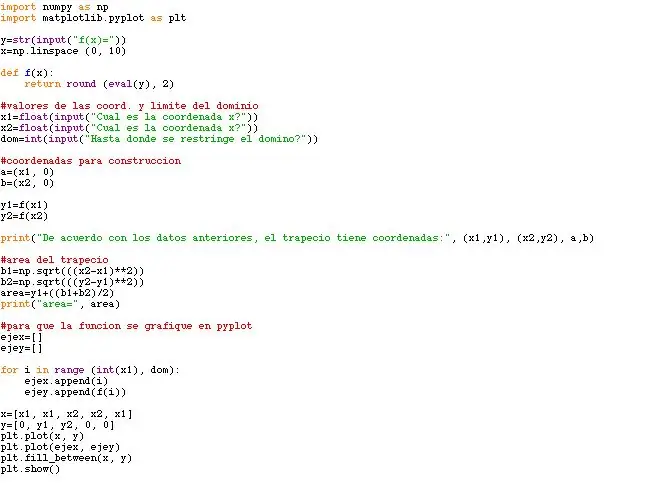
Passo 1: Importar Bibliotecas

Este programa requer as bibliotecas dentro do programa: matplotlib.pyplot y pylab. En la foto adjunta a este paso se puede ver que haciendo o uso de los comandos from, import y as el programa puede acceder to la información de las das librerías utilizadas por este programa.

da importação pylab

import matplotlib.pyplot as plt

IMPORTANTE: ¡POR FAVOR NO PONGAS TILDES EN NINGUNA PALABRA NI NINGÚN SÍMBOLO DEL ESPAÑOL! DE LO CONTRARIO SE CERRARÁ EL PROGRAMA Y NÃO SE GUARDARÁN LOS CAMBIOS QUE HICISTE

Etapa 2: Evalúa La Función

Hay ciertas cosas que não puedes calcular sin saber ciertos datos que el programa no te puede dar, a menos que le preguntes al usuario (es decir el que va a utilizar el programa después de su creación) los valores de ciertas variables; en este caso debemos preguntarle al usuario por la función a la cual le quieras calcular el área.

Para predefinir o usuário para o tipo de função, debes hacer uso do fluxo de comandos (str) e entrada. stream es um comando que permite introduzir variáveis algebraicas (como "x" y "y") dentro de um conjunto numérico y que se entiendan como números desconocidos dentro de la ecuación, es decir que permite calcular, por ejemplo, x ^ 2 + 5 y que entienda a "x" como um número que no se conoce. Por outro lado, a entrada permite que o valor que introduza o programa pré-definido para o mar variável, o que adquire para o resto do programa. La función linspace sirve para restringir los valores del eje a los indicados dentro do paréntesis.

Neste caso, é necessário definir a variável "e" por meio de uma função

y = str (input ("f (x) ="))

x = np.linspace (0, 10) def f (x): volta de retorno (eval (y), 2)

Etapa 3: Variáveis Asigna De Las Coordenadas

Para que as coordenadas cartesianas se puedan graficar, es necesario que o programa pregunte al usuario los valores que toma la función en el eje x. Dado que estos son valores valores enteros, se debe volver a usar input, que permite que o valor que introduzcas cuando o programa pregunte a variável mar o que adquira o resto do programa. Para que o programa pregunte as variáveis cuando lo pongas a funcionar, debes usar print para que la pregunta aparezca en la ventana SHELL. Neste caso, se necessário saber os valores de x e a restrição do domínio.

Recuerda that el dominio son los values del eje x en una función.

#valores de las coord. y limite del dominiox1 = float (input ("Cual é a coordenada x?")) x2 = float (input ("Cual é a coordenada x?")) dom = int (input ("Hasta donde se restringe el domino?"))

Etapa 4: Construcción Del Trapecio Según Coordenadas Y Función

Para construir el polígono, ya se tienen los valores that adquiere la función en x. Ahora, para os valores de y y (x1, 0) y (x2, 0), se le asigna con las variáveis y = f (x) y otro nombre para las previamente mencionadas.

#coordenadas para construcciona = (x1, 0) b = (x2, 0) y1 = f (x1) y2 = f (x2)

print ("De acuerdo con los datos anteriores, el trapecio tiene coordenadas:", (x1, y1), (x2, y2), a, b)

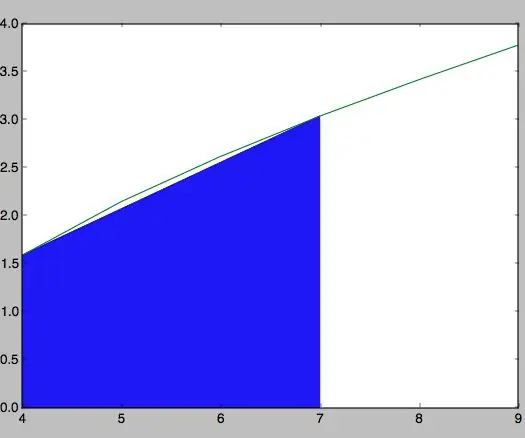
Etapa 5: Calcular El Área Del Trapecio Dentro De La Función

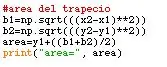
Para este paso, se debe tener en cuenta la forma del trapecio, es decir, que tiene dos bases y la altura. As bases neste caso são obtidas por meio de la raíz cuadrada de la resta de los valores de x1 y x2 al cuadrado. Lo mismo ocurre para os valores de y1 e y2.

Para hallar el área total, es la suma de la altura y las bases sobre dos.

#area del trapeciob1 = np.sqrt (((x2-x1) ** 2)) b2 = np.sqrt (((y2-y1) ** 2)) área = y1 + ((b1 + b2) / 2) imprimir ("área =", área)

Etapa 6: Gráfica em Pyplot

#para que a função se grafique em pyplot

ejex =

ejey =

para i no intervalo (int (x1), dom):

ejex.append (i) ejey.append (f (i))

Para que a função se grafique hay que asignar los ejes x e y, pero como ya hay muchas variáveis con esos nombres, asigna unos que identifiques como los ejes y não otras variáveis. El condicional para i no intervalo organiza la función de acuerdo con los parámetros estabelecidos al inicio del programa.

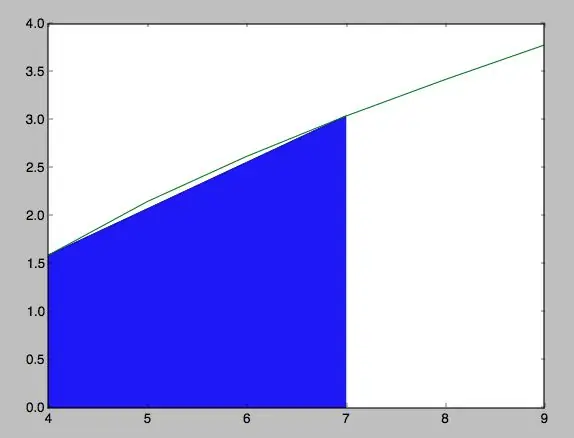
Etapa 7: Organización De La Gráfica

x = [x1, x1, x2, x2, x1] y = [0, y1, y2, 0, 0]

plt.plot (x, y)

plt.plot (ejex, ejey) plt.fill_between (x, y) plt.show ()

Este é o passado para organizar as coordenadas de manera que coincide com a gráfica em seus respectivos ejes. Por outro lado, se você encontrar o espaço do trapézio e se vai calcular a área e se muestra la gráfica.

Etapa 8: ¡Lo Lograste

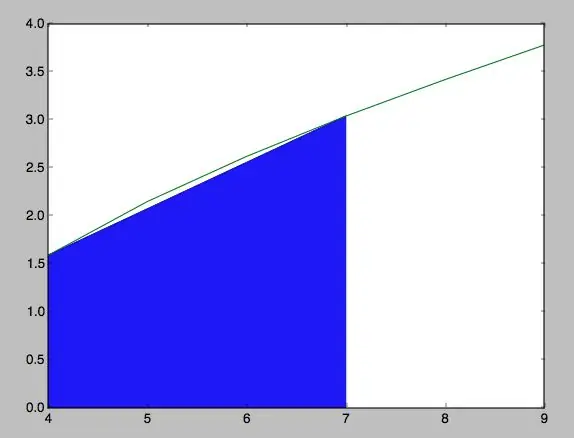
Después de haber seguido todos los pasos, encontrarás que tu programa debe ser muy similar to lo que hay en las fotos adjuntas. Obviamente, los valores de las coordenadas y la función varían según como tú quieras ponerlos, y por ende, el área y la forma de la curva.