Análise de bioimpedância (BIA) com o AD5933: 9 etapas

2024 Autor: John Day | [email protected]. Última modificação: 2024-01-30 11:37

Estou interessado em fazer um Analisador de Bioimpedância para medições de composição corporal e minhas pesquisas aleatórias continuaram encontrando um projeto da aula de Instrumentação Biomédica de 2015 na Universidade de Vanderbilt. Eu trabalhei no design e o melhorei um pouco. Eu gostaria de compartilhar minhas descobertas com você. Veja o que você pode usar neste "passo-a-passo", se algo não estiver claro, sugira melhorias. Posso um dia escrever meu pensamento de uma forma mais coesa, mas por agora espero que você possa usar tudo o que vir aqui. (Se você acha que pode escrever isso e melhorar, você é bem-vindo)

Urso de pelúcia

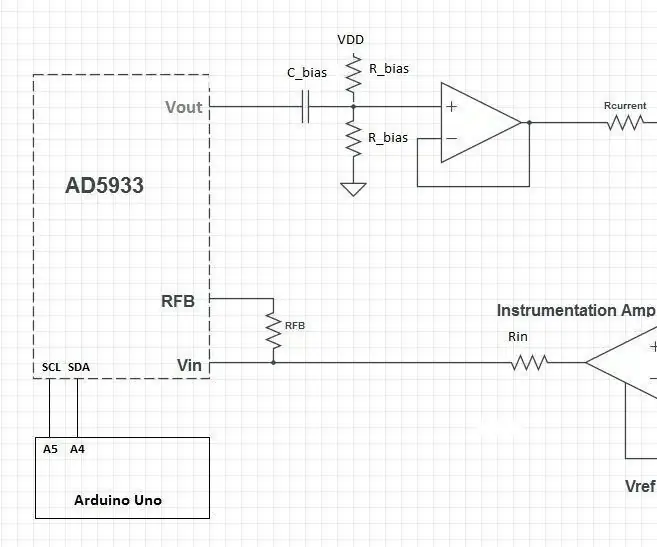
Este projeto consiste no chip AD5933 e um front-end analógico personalizado (AFE) para fazer a interface do AD5933 com o corpo. O AD5933 então faz a medição e os resultados podem ser processados por um microcontrolador (por exemplo, um Arduino).

Se você planeja usar o Arduino como fonte de alimentação, certifique-se de que os amplificadores operacionais e de instrumentação (op-amps e in-amps) suportem as chamadas tensões de "fonte única" e tenham especificações de trilho a trilho.

(A seguir, estarei usando uma fonte de alimentação (de um Arduino) de 5 V e a configuração de Faixa 1 no AD5933.)

Etapa 1: O Estágio de Re-polarização

A primeira parte do AFE é um estágio de polarização. O sinal de tensão de saída não está centralizado no meio da faixa de tensão de alimentação (VDD / 2). Isso é corrigido usando um capacitor para bloquear a parte CC do sinal e enviá-lo por meio de um divisor de tensão para adicionar um deslocamento CC de volta ao sinal.

Os dois resistores de polarização podem ter qualquer valor, desde que sejam iguais. O valor específico do limite também não é importante.

O estágio de re-bias funciona como um filtro passa-altas e, portanto, tem uma frequência de corte:

f_c = 1 / (2 * pi * (0,5 * R) * C)

Certifique-se de que a frequência de corte esteja algumas décadas abaixo da frequência mínima que você planeja usar. Se você planeja usar 1kHz em sua aplicação, escolha limites e valores de resistor que fornecerão uma frequência de corte da ordem de 1-10 Hz.

A última parte deste estágio é um amplificador operacional configurado para ser um seguidor de tensão. Isso é para garantir que os valores do resistor não interfiram com o próximo estágio

Etapa 2: Resistor de detecção de corrente

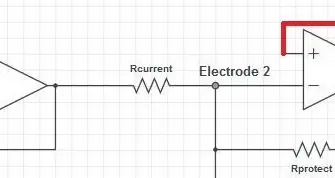
A primeira parte do próximo estágio é o resistor de detecção de corrente. A corrente através deste resistor será a mesma corrente que o amplificador tentará manter através do corpo. Certifique-se de que a corrente esteja em conformidade com os padrões de segurança IEC6060-1 *:

Abaixo das frequências de 1 kHz, um máximo de 10 microAmps (RMS) são permitidos no corpo. Em frequências acima de 1kHz, a seguinte equação fornece a corrente máxima permitida:

Corrente CA máx. <(Frequência mínima em kHz) * 10 microAmps (RMS)

A relação entre a amplitude de pico de um sinal AC e seu valor RMS é: Peak = sqrt (2) * RMS. (10 microAmps RMS correspondem a 14 microAmps de amplitude de pico)

Usando a Lei dos Ohms no resistor, podemos calcular o valor do resistor que atenderá ao padrão de segurança. Usamos a tensão de excitação do AD5933 e o valor máximo da corrente:

U = R * I => R = U / I

Por exemplo. usando a configuração da Faixa 1 Upeak = 3V / 2 = 1,5V (ou 1V @ 3,3V)

Usando o valor de pico de 14 microAmp acima, obtenho um valor de resistor de pelo menos 107 kOhms

Referências:

* Dispositivos analógicos: "Projeto de circuito de bioimpedância para sistemas usados no corpo"

Etapa 3: O amplificador de trans-condutância

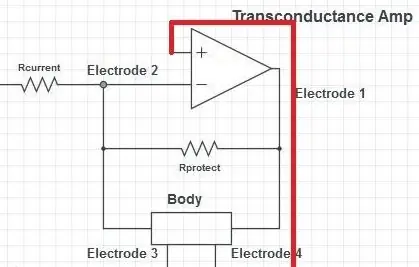
Após o resistor de detecção de corrente, há um amplificador operacional em uma configuração de feedback negativo. Esta é uma configuração chamada Load-in-the-Loop. O terminal de entrada positivo do amplificador operacional é conectado a uma tensão VDD / 2. O amplificador operacional agora tentará ajustar sua saída na direção oposta ao sinal de excitação de forma que a tensão no terminal negativo seja igual a VDD / 2. Isso produzirá um potencial de oscilação, empurrando e puxando a corrente através do corpo.

A corrente retirada do terminal negativo do op-amp é virtualmente zero. Toda a corrente através do resistor de detecção de corrente, portanto, deve fluir através do corpo. Este é o mecanismo que torna esta configuração um amplificador de trans-condutância (também chamado de fonte de corrente controlada por tensão, VCCS).

O op-amp só pode manter a corrente se a impedância do corpo não for muito alta. Caso contrário, a saída do amplificador operacional seria apenas máxima na tensão de alimentação (0 ou 5 V). A amplitude de tensão máxima que pode ser mantida é VDD / 2 + Upeak (2,5 + 1,5 V = alimentação 4 V @ 5 V). As margens de tensão do amplificador operacional devem ser subtraídas deste valor, mas se o amplificador operacional tiver especificações de trilho a trilho, isso seria apenas uma pequena quantidade. A impedância máxima que o amplificador operacional pode conduzir é, portanto:

Z <(VDD / 2 + Upeak) / Imax

(Na minha configuração Z <4V / 14 microAmps = 285 kOhms, desejo é suficiente para cobrir a faixa de impedância do corpo)

O resistor protetor tem um valor muito grande (1-1,5 MOhms) em comparação com o corpo (aproximadamente 100kOhms) e para todas as operações normais isso não puxará nenhuma corrente perceptível e a impedância da conexão paralela é dominada pela impedância do corpo. Se a impedância do corpo aumentar (por exemplo, almofadas se soltando), a corrente pode então passar pelo resistor e a saída máxima do amplificador operacional não criaria tensões desagradáveis nas almofadas.

Etapa 4: o amplificador de instrumentação

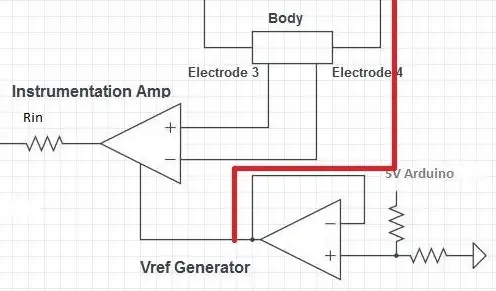
O próximo estágio é o amplificador de instrumentação (in-amp) que mede a voltagem em todo o corpo. A tensão em todo o corpo está oscilando em torno de 0 V, mas o AD5933 precisa que a tensão de entrada esteja em uma faixa positiva. Portanto, o amplificador de entrada adiciona um deslocamento CC de VDD / 2 ao sinal de tensão medido.

A referência VDD / 2 é gerada por um divisor de tensão. Qualquer valor de resistor pode ser usado, desde que sejam iguais. O divisor de tensão é separado da impedância do resto do circuito por um seguidor de tensão. A saída do seguidor de tensão pode então ser encaminhada para o amplificador de entrada e para o amplificador de trans-condutância.

Etapa 5: o estágio de entrada e calibração

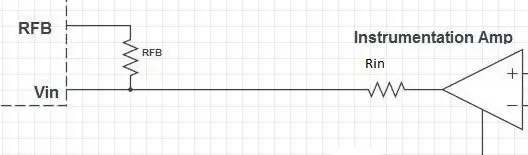
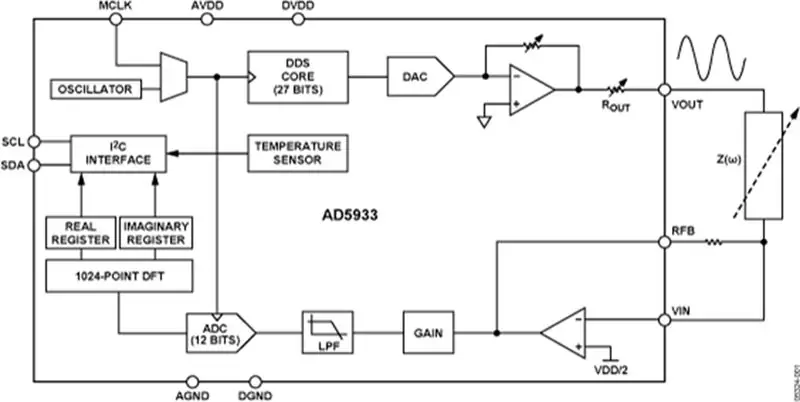
O estágio de entrada do AD5933 contém um amplificador operacional em configuração de feedback negativo. Existem dois resistores: um em série (Rin) e um em paralelo (RFB). O ganho do op-amp é dado por

A = - RFB / Rin

Os ganhos do op-amp de entrada e do in-amp (e PGA) precisam ter certeza de que o sinal que vai para o ADC do AD5933 está sempre entre 0V e VDD.

(Eu uso um ganho de unidade em amp e valores de resistor que darão aproximadamente A = 0,5)

Dentro do AD5933, o ADC converterá o sinal de tensão em um sinal digital. A faixa de tensão de 0 V a VDD é convertida para a faixa digital de 0-128 (2 ^ 7). (A documentação não é clara sobre isso, mas um exame atento das parcelas em [1] e alguns experimentos de minha parte confirmam isso.)

Dentro do módulo DFT existe outra escala de 256 (1024/4, veja [1]) antes que o resultado seja salvo no registro real e imaginário.

Seguindo o sinal de tensão através do AFE, no ADC e usando os fatores de escala mencionados antes, é possível estimar o fator de ganho como sendo:

g = (VDD * Rcurrent * Rin) / (256 * PGA * Upeak * RFB * 2 ^ 7)

alguma calibração ainda pode ser necessária, portanto, leve em consideração alguns efeitos que não fazem parte deste modelo matemático, portanto, meça o valor real do ganho medindo componentes de impedância conhecida, como resistores. (g = Z / mag, veja abaixo)

A impedância agora pode ser calculada por

Z = g * mag

mag = sqrt (real ^ 2 + imaginário ^ 2)

PA = arctan2 (real, imaginário) - deltaPA

O PA provavelmente precisa ser calibrado, assim como há uma mudança de fase sistemática em função da frequência no AD5933. deltaPA provavelmente será alguma função linear de frequência.

A resistência e reatância agora podem ser calculadas por

R = Z * cos (PA)

X = Z * sin (PA)

Referências: [1] Leonid Matsiev, "Improving Performance and Versatility of Systems Based on Single-Frequency DFT Detectors such as AD5933", Electronics 2015, 4, 1-34; doi: 10.3390 / electronics4010001

Etapa 6: Material Avançado: Vazamento Espectral (DC)

O sinal que colocamos no AD5933 é uma tensão / corrente como função de tempo, mas nosso principal interesse é a impedância como função de frequência. Para converter entre o domínio do tempo e o domínio da frequência, precisamos obter a transformada de Fourier do sinal no domínio do tempo. O AD5933 tem um módulo integrado de transformada discreta de Fourier (DFT). Em baixas frequências (abaixo de aproximadamente 10 kHz), a construção em DFT é influenciada por aliasing e vazamentos espectrais. Em [1] ele aborda a matemática de como corrigir o vazamento espectral. A essência disso é calcular cinco (mais duas) constantes para cada passo de frequência na varredura. Isso pode ser feito facilmente, por exemplo, pelo Arduino em software.

O vazamento vem em duas formas: um vazamento DC que é aditivo por natureza e um vazamento AC que é multiplicativo por natureza.

O vazamento DC decorre do fato de que o sinal de tensão no ADC não está oscilando em torno de 0 V, mas em torno de VDD / 2. Um nível DC de VDD / 2 deve corresponder a uma leitura DC digital de aproximadamente 64 (delta designado em [1]).

As etapas para corrigir o vazamento espectral DC:

1) Calcule o fator de envelope E para a frequência atual.

2) Calcule os dois fatores de ganho GI (real) e GQ (imaginário)

3) Subtraia delta * GI do valor do registro real e delta * GQ do valor do registro imaginário

Referências:

[1] Leonid Matsiev, "Improving Performance and Versatility of Systems Based on

Detectores DFT de frequência única, como AD5933 , Electronics 2015, 4, 1-34; doi: 10.3390 / electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Medidas Syst., Vol. XXII (2015), No. 1, pp. 13–24.

Etapa 7: Material Avançado: Vazamento Espectral (AC)

Como o vazamento DC, o vazamento AC pode ser corrigido matematicamente. Em [1] a resistência e a reatância são denominadas A * cos (phi) e A * sin (phi) respectivamente, onde A corresponde à magnitude da impedância e phi corresponde ao ângulo de fase (PA).

As etapas para corrigir o vazamento espectral AC:

1) Calcule o fator de envelope E (diferente de DC) para a frequência atual.

2) Calcule os três fatores a, b e d. (valores aproximados em frequências mais altas: a = d = 256 eb = 0)

3) Resistência (Acos (phi)) e reatância (Asin (phi)) agora podem ser calculadas em unidades digitais

Referências: [1] Leonid Matsiev, "Improving Performance and Versatility of Systems Based on Single-Frequency DFT Detectors such as AD5933", Electronics 2015, 4, 1-34; doi: 10.3390 / electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Medidas Syst., Vol. XXII (2015), No. 1, pp. 13–24.

Etapa 8: Coisas Avançadas: o fator de ganho teórico

Dada a modelagem matemática do DFT, também deve ser possível modelar matematicamente todo o AFE. Matematicamente, o sinal de tensão pode ser descrito por uma função seno com uma determinada frequência fixa, um deslocamento CC e uma oscilação CA com uma amplitude de pico. A frequência não muda durante um passo de frequência. Como o fator de ganho apenas altera a magnitude da impedância e não o PA, não vamos nos preocupar aqui com qualquer mudança de fase induzida no sinal.

Aqui está um breve resumo do sinal de tensão à medida que se propaga através do AFE:

1) Após o estágio de redefinição, a amplitude AC ainda é Upeak = 1,5V (1V @ VDD = 3,3V) e o offcet DC foi alterado para VDD / 2.

2) No resistor de detecção de corrente, a tensão ainda é a mesma do estágio anterior …

3) … mas devido à voltagem gangorra do amplificador operacional, as oscilações CA têm um tamanho de Z * Upeak / Rcurrent. (O deslocamento DC é cancelado pela tensão de referência do amplificador operacional de VDD / 2 - o ponto de articulação da gangorra - e se torna um aterramento virtuel nesta parte do circuito)

4) A unidade in-amp adiciona o deslocamento DC de VDD / 2 de volta e encaminha o sinal para o estágio de entrada do AD5933

5) O op-amp no estágio de entrada tem um ganho de A = -RFB / Rin e a amplitude AC, portanto, torna-se (Z * Upeak / Rcurrent) * (RFB / Rin)

6) Pouco antes do ADC, há um amplificador de ganho programável (PGA) com duas configurações de ganho de 1 ou 5. O sinal de tensão no ADC torna-se: PGA * (Z * Upeak / Rcurrent) * (RFB / Rin)

O ADC converte o sinal v (t) em um sinal digital x (t) = u (t) / VDD * 2 ^ 7 com uma precisão de 12 bits.

A magnitude A é conectada à impedância Z pelo fator de ganho, k, como A = k * Z e tem um valor aproximado de k = PGA * Upeak * RFB * 2 ^ 7 / (VDD * Rcurrent * Rin).

Se você gosta de trabalhar com ganho-faktor em vez de g = 1 / k e Z = g * A.

Etapa 9: Coisas Avançadas: a Mudança PA

Em [2] eles encontram uma mudança sistemática no PA em função da frequência. Isso se deve a um atraso de tempo entre o DAC, onde o sinal de excitação é gerado, e o DFT, onde o sinal de entrada precisa ser complicado com o sinal de saída.

A mudança é caracterizada pelo número de ciclos de clock em que o sinal está atrasado entre o DAC e o DFT internamente no AD5933.

Referências: [1] Leonid Matsiev, "Improving Performance and Versatility of Systems Based on Single-Frequency DFT Detectors such as AD5933", Electronics 2015, 4, 1-34; doi: 10.3390 / electronics4010001

[2] Konrad Chabowski, Tomasz Piasecki, Andrzej Dzierka, Karol Nitsch, "Simple Wide Frequency Range Impedance Meter Based on AD5933 Integrated Circuit", Metrol. Medidas Syst., Vol. XXII (2015), No. 1, pp. 13–24.