
Índice:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:38.
- Última modificação 2025-01-23 15:03.

Quando eu era criança, peguei um livro que era dos meus pais, chamado The Scientific American Book Of Projects For The Amador Scientist. Ainda tenho o livro e, pelo que sei, é um livro difícil de encontrar hoje em dia. Mas você pode ler online agora. Este livro serviu para me apresentar a muitas coisas, mas o capítulo que despertou meu interesse foi aquele sobre Máquinas matemáticas. Pode muito bem ser a única coisa que me iniciou na minha carreira eventual de desenvolvimento de software.
Neste capítulo, há descrições de máquinas de resolução de quebra-cabeças usando circuitos da época … que antecederam os circuitos integrados modernos ou mesmo transistores (usando relés). Mas alguns dos mesmos conceitos estavam lá, os de dispositivos lógicos que são essencialmente a mesma coisa que os computadores modernos ainda usam hoje.
Hoje em dia, você pode obter sistemas inteiros de computador de maneira fácil e barata por alguns dólares e apenas programar seu quebra-cabeça ou jogo. Mas você também pode fazer muitas coisas em um nível inferior, usando as portas lógicas a partir das quais os computadores são construídos, para criar hardware personalizado para seu quebra-cabeça. Embora isso possa não ser prático ou ideal, permite que você aprenda como os computadores realmente funcionam. Também é divertido.
Etapa 1: Materiais necessários
Você pode construir isso inteiramente em Circuitos Tinkercad e simular o funcionamento real do quebra-cabeça.
Se você deseja construí-lo fisicamente, aqui está o que você precisa:
4 interruptores ou interruptores deslizantes.
1 botão (momentâneo)
2 placas de ensaio pequenas.
9 LEDs.
9 resistores de 1K.
1 7475 quad latch chip
2 7408 quad E portões
1 7432 quad OR gate
1 bateria com 3 células AA ou AAA.
conjunto de fios de jumper.
Para os chips da série 74xx, você pode usar qualquer variação deles. Ou seja, as versões 74xx são o TTL original, mas você também pode usar as versões 74LSxx (menor consumo de energia) ou 74HCxx (versões CMOS de energia ainda mais baixa) etc. Lembre-se de que as versões 74xx e 74LSxx são fáceis de manusear, mas todas as outras variações são eletricidade estática sensível.
Etapa 2: lógica booleana


A lógica booleana pode parecer assustadora, mas na verdade é muito simples. Booleano significa apenas que você está lidando com apenas 1s e 0s, ou Verdadeiro e Falso. Ou em eletrônica, + e -. A parte lógica disso se resume a muito "se isso então aquilo". As operações lógicas mais básicas são simplesmente essas três coisas: AND, OR e NOT. Esses são chamados de portões, porque atuam essencialmente como portais literais para o fluxo de eletricidade através de um circuito.
A porta AND funciona da seguinte maneira. Possui duas entradas e uma saída. As duas entradas podem ser 1 ou 0, e a saída é 1 ou 0. Para a porta AND, se ambas as entradas são 1, a saída é 1. Caso contrário, a saída é 0.
Para a porta OR, também possui duas entradas e uma saída. Se uma ou outra entrada for 1, a saída será 1.
A porta final é a porta NOT, e ela tem apenas uma entrada e uma saída. Se a entrada for 1, a saída será 0. Se a entrada for 0, ela gerará 1.
As portas OR e AND também podem ter mais de 2 entradas. Para simplificação, eles podem ser mostrados com 2 ou mais linhas entrando em uma porta, mas na verdade, uma porta de 3 entradas é apenas duas portas de 2 entradas com uma alimentando a outra.
Agora você sabe tudo o que precisa saber para construir um computador. Mesmo os computadores mais modernos usam apenas essas três coisas, embora possam usar milhões delas.
Então, vamos construir um quebra-cabeça.
Etapa 3: Quebra-cabeça do fazendeiro, raposa, ganso e grãos

A primeira coisa no livro é um circuito lógico para criar o quebra-cabeça clássico do Fazendeiro, da Raposa, do Ganso e do Grão. Este quebra-cabeça existe há centenas de anos em diferentes formas. É um quebra-cabeça básico de lógica com apenas algumas regras. O quebra-cabeça é o seguinte.
Um fazendeiro tem uma raposa, um ganso e alguns grãos. Ele chega a um rio que deve cruzar, e há um barco, mas ele só pode segurá-lo e uma outra coisa de cada vez.
Ele não pode deixar a raposa com o ganso, porque a raposa comerá o ganso. Isso é o que as raposas fazem, é apenas sua natureza.
Ele não pode deixar o ganso com o grão, porque o ganso vai comê-lo.
Como ele pode levar os três para o outro lado do rio com segurança?
Para criar esse quebra-cabeça, precisamos de algumas coisas. Primeiro, comece com quatro interruptores, um para cada agricultor, raposa, ganso e grão. É assim que definiremos o que vai para o barco.
Em segundo lugar, precisamos do quebra-cabeça para lembrar onde tudo está, passo a passo.
Em seguida, precisamos de um botão para dizer quando mover o barco.
Finalmente, precisamos de alguma lógica para fazer cumprir as regras.
Etapa 4: Memória


Para lembrar a localização dos objetos neste quebra-cabeça, usaremos algo mais avançado do que os relés usados no circuito original. Na época em que este livro foi escrito, não havia transistores, mas eles tinham relés. Esses relés eram conectados de forma que, quando você pressionava um botão, eles fechavam e permaneciam fechados até que você pressionasse o botão do outro lado.
Hoje usaremos uma peça comum e barata chamada trava de 4 bits. Um 'bit' na lógica do computador refere-se apenas a um único 1 ou 0. É a mesma coisa que um dígito. Este Circuito Integrado (ou "IC" ou "Chip") contém 4 componentes lógicos conhecidos como flip-flops. Um flip-flop é apenas um par de portas configuradas de forma que, quando você atribuir a ele 1 ou 0 como entrada, ele produzirá 1 ou 0 e ficará 'travado'. Daí o nome flip / flop. Ele vai mudar de 1 para 0 ou flop de 0 para 1 (ou é o contrário?) E então permanecerá lá. Isso basicamente faz a mesma coisa que os quatro relés do circuito antigo.
Você pode fazer um flip-flop simples com apenas duas portas, mas as que estão nesta trava têm um recurso extra (requer mais algumas portas). Em vez de ter a mudança de saída imediatamente com a mudança de entrada, ele tem uma outra entrada que habilita ou desabilita as entradas. Normalmente, ele permanece desativado. Isso permite que você defina dois dos interruptores (o fazendeiro e um outro) antes de tentar 'enviar' o barco para o outro lado. Nosso circuito já é mais inteligente que o antigo.
Agora temos a capacidade de definir e lembrar as localizações de todos os princípios de nosso quebra-cabeça.
Aqui está nosso circuito até agora: trava de 4 bits
Etapa 5: lógica de regras

Para impor as regras e indicar quando há um problema, usaremos algumas portas lógicas booleanas para implementar as restrições de que precisamos.
Precisaremos de quatro testes para determinar se há um problema - se algum deles for verdadeiro, acenda o sinal de alerta.
1. Se o grão e o ganso estão do outro lado do rio e não o fazendeiro.
2. Se a raposa e o ganso estão do outro lado do rio e não o fazendeiro.
3. Se o fazendeiro cruzar o rio e nenhuma raposa e nenhum ganso estiverem com ele.
4. Se o fazendeiro cruzar o rio e nenhum grão e nenhum ganso estiverem com ele.
Observe a maneira como expressei isso para corresponder exatamente à lógica que usaremos, que são portas AND com as saídas normais ou invertidas da trava, as invertidas agindo como um "não" ou um "NÃO".
Uma vez que qualquer um deles pode ser verdadeiro, causando um problema, todos eles alimentam uma porta OR.
A lógica concluída, incluindo a trava de 4 bits, é mostrada na captura de tela. Isso vem de um programa chamado logicaly. Este programa é excelente para mostrar o fluxo da lógica conforme você manipula os interruptores, destacando em azul as conexões com valor '1'. Anexei o arquivo que você pode carregar logicamente.
Etapa 6: protótipo de um circuito real

Agora podemos criar um circuito de trabalho real. Usando os circuitos do Tinkercad, podemos fazer isso simulando a aparência real e a funcionalidade do hardware.
A Tinkercad tem uma trava 7475 de 4 bits embutida, para que essa parte seja fácil. Para as portas, escolhi usar dois chips com 4 portas AND cada (o 7408). Para criar quatro portas AND de 3 entradas, usamos duas portas AND com a saída de uma indo para 1 entrada da outra. Isso deixa 1 entrada na segunda e 2 entradas na primeira, criando uma porta AND de 3 entradas. Para o portão de cirurgia, eu faço a mesma coisa. Um chip de quatro portas OR usa duas portas OR com as saídas indo para uma terceira porta OR. Um portão não é usado.
Execute a simulação em circuitos Tinkercad
Recomendado:
Lembrete de quebra de conforto Tele-LED de 1963: 4 etapas (com fotos)

1963 Tele-LED Comfort Break Reminder: Este antigo e incomum telefone sem discagem agora ajuda o bem-estar e a produtividade a coexistir no escritório em casa! Abaixo de sua grade vintage, um anel de neopixel acende seus 24 LEDs em sequência por uma hora, mudando para uma tela de arco-íris atraente quando
Quebra-nozes cantando Arduino: 8 etapas

Singing Arduino Nutcracker: Este quebra-nozes abre sua boca com base no áudio de entrada. Isso pode ser feito facilmente em menos de 3 horas para um iniciante ir de uma pilha de peças a um quebra-nozes cantante. Para este projeto, você vai precisar de um quebra-nozes com uma boca móvel, um protótipo
Circuito de alarme de quebra de fio com IRFZ44N MOSFET: 11 etapas
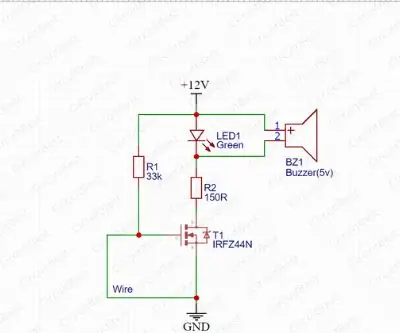
Circuito de alarme de quebra de fio com IRFZ44N MOSFET: Hoje, durante este artigo, tendemos a medir o quadrado e discutir os benefícios do circuito de alarme de quebra de fio com IRFZ44N MOSFET. O IRFZ44N é associado em enfermagem N-Channel adoçante tipo MOSFET para isso entregará alto rendimento para straightf
Raposa carmesim: aumentando a conscientização para fazer uma pausa durante o trabalho: 8 etapas (com fotos)

Crimson Fox: Aumentando a Conscientização para Fazer uma Pausa Durante o Trabalho: Para um curso que seguimos na KTH na Suécia, fomos designados para criar um artefato que poderia mudar de forma. Fizemos um artefato em forma de raposa, supostamente para lembrá-lo de fazer uma pausa no trabalho ou nos estudos. O conceito geral é que a raposa exibirá
Alarme de quebra de vidro / alarme contra roubo: 17 etapas

Alarme de quebra de vidro / Alarme de roubo: Este circuito pode ser usado para soar um alarme para detectar a quebra de uma janela de vidro por um intruso, mesmo quando o intruso garante que não haja som do vidro quebrado
