
Índice:
- Etapa 1: gerar uma matriz NxN de quadrados uniformes
- Etapa 2: randomizando a rede
- Etapa 3: Obtenha novas distâncias
- Etapa 4: Selecione um ponto e compare a distância desse ponto a outros
- Etapa 5: mover para um novo ponto
- Etapa 6: Força = distância K *
- Etapa 7: Mude o movimento da rede devido ao ponto movido
- Etapa 8: Código Concluído
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:38.
- Última modificação 2025-01-23 15:03.

As células são capazes de interagir com sua matriz extracelular circundante (ECM) e podem tanto se aplicar como responder às forças exercidas pela ECM. Para o nosso projeto, simulamos uma rede interligada de fibras que atuariam como o ECM e vemos como a rede muda em resposta ao movimento de um dos pontos. O ECM é modelado como um sistema interligado de molas que estão inicialmente em equilíbrio com uma força líquida de zero. Como a força é aplicada à rede em resposta ao movimento do ponto, tentamos fazer com que os pontos conectados reajam à força de tal forma que tentem retornar ao equilíbrio. A força é monitorada pela equação F = k * x onde k é a constante da mola ex é a mudança no comprimento da fibra. Esta simulação pode ajudar a dar uma compreensão geral da propagação de força em redes fibrosas que podem eventualmente ser usadas para ajudar a simular a mecanotransdução.
Etapa 1: gerar uma matriz NxN de quadrados uniformes


Para começar o código, escolhemos N que vai determinar as dimensões da nossa rede (NxN). O valor de N pode ser alterado manualmente para alterar as dimensões da rede conforme necessário. Neste exemplo, N = 8, portanto, temos uma rede de pontos de 8x8. Depois de gerar a matriz, conectamos todos os pontos na matriz que têm um comprimento de 1 unidade usando a fórmula da distância, distância = sqrt ((x2-x1) ^ 2 + (y2-y1) ^ 2). Fazendo isso, obtemos uma rede de quadrados que são todos igualmente espaçados por 1 unidade. Isso pode ser visto na figura 101.
Etapa 2: randomizando a rede


Nesta etapa, queremos randomizar todas as localizações dos pontos, exceto os pontos externos que formarão nosso limite. Para fazer isso, primeiro encontramos todas as coordenadas da matriz que são iguais a 0 ou N. Esses pontos são os que constituem o limite. Para os pontos não-limite, a localização é aleatória adicionando um valor aleatório diferente de -.5 a.5 para ambas as posições xe y. A imagem aleatória plotada pode ser vista na Figura 1.
Etapa 3: Obtenha novas distâncias

Uma vez que nossa rede aleatória é feita, encontramos a distância entre os pontos conectados usando a fórmula da distância novamente.
Etapa 4: Selecione um ponto e compare a distância desse ponto a outros



Nesta etapa, podemos selecionar um ponto de interesse usando o cursor, conforme mostrado na Figura 2. Você não precisa mover o cursor exatamente para o ponto porque o código o ajustará para o ponto de conexão mais próximo. Para fazer isso, primeiro calculamos a distância entre todos os pontos conectados e o ponto que acabamos de selecionar. Depois que todas as distâncias são calculadas, selecionamos o ponto com a menor distância do ponto selecionado para se tornar o ponto selecionado real.
Etapa 5: mover para um novo ponto



Nesta etapa, usando o ponto que foi selecionado na etapa anterior, movemos o ponto para um novo local. Este movimento é feito selecionando uma nova posição com o cursor que substituirá a posição anterior. Este movimento será usado para simular uma força exercida devido à mudança no comprimento da mola. Na figura toda azul, um novo local está sendo selecionado. Na próxima figura, o movimento pode ser visualizado pelas conexões laranja, que são as novas localizações, em oposição às conexões azuis, que eram as antigas localizações.
Etapa 6: Força = distância K *

Nesta etapa, aplicamos a equação força = k * distância, onde k é uma constante 10 para as fibras de colágeno. Como a rede de fibras começa em seu estado de equilíbrio, a força resultante é 0. Criamos um vetor zero do comprimento da matriz que geramos anteriormente para representar esse equilíbrio.
Etapa 7: Mude o movimento da rede devido ao ponto movido




Nesta etapa, simulamos o movimento da rede em resposta ao movimento do ponto para retornar ao seu estado de equilíbrio. Começamos encontrando as novas distâncias entre dois pontos. Com isso, podemos encontrar a mudança no comprimento da fibra observando a diferença entre as distâncias antigas e novas. Também podemos ver quais pontos foram movidos e também os pontos aos quais eles estão conectados, comparando as localizações dos pontos novos e antigos. Isso nos permite ver quais pontos devem se mover em resposta à força exercida. A direção do movimento pode ser dividida em seus componentes xey, dando um vetor de direção 2D. Usando o valor k, a mudança na distância e o vetor de direção, podemos calcular o vetor de força que pode ser usado para mover nossos pontos em direção ao equilíbrio. Executamos esta seção do código 100 vezes, cada vez movendo em incrementos de Força *.1. Executar o código 100 vezes nos permite finalmente alcançar o equilíbrio novamente e, ao manter as condições de contorno, vemos uma mudança na rede em vez de simplesmente uma mudança inteira. O movimento da rede pode ser visto na Figura 3 com o amarelo sendo as posições movidas e o azul sendo as anteriores.
Etapa 8: Código Concluído
Anexado nesta seção está uma cópia do nosso código. Sinta-se à vontade para modificá-lo para atender às suas necessidades com a modelagem de várias redes!
Recomendado:
Descubra quando alguém entrou em uma sala usando o sensor de radar Xyc-wb-dc: 7 etapas

Descubra quando alguém entrou em uma sala usando o sensor de radar Xyc-wb-dc: Neste tutorial, aprenderemos como descobrir quando alguém entrou em uma sala usando o módulo RTC, sensor de radar xyc-wb-dc, display OLED e arduino. vídeo de demonstração
Sensor ultrassônico para capturar mudanças de posição de objetos: 3 etapas

Sensor Ultrassônico para Captura de Mudanças de Posicionamento de Objetos: É importante manter suas coisas valiosas seguras, seria ruim se você continuasse guardando seu castelo o dia todo. Usando a câmera raspberry pi você pode tirar as fotos no momento certo. Este guia o ajudará a gravar um vídeo ou tirar uma foto
Medindo o peso com uma célula de carga: 9 etapas
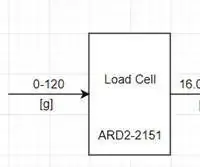
Medindo Peso com uma Célula de Carga: Esta postagem irá cobrir como configurar, solucionar problemas e reorganizar um circuito para medir pesos abaixo de 1kg. Um ARD2-2151 custa € 9,50 e pode ser comprado em: https: //www.wiltronics .com.au / product / 9279 / load-ce … O que foi usado: -A 1Kg Load Cell (ARD2-2151)
Ligue um celular / telefone móvel com bateria externa ou rede elétrica: 3 etapas

Alimentar um celular / telefone móvel com bateria externa ou rede elétrica .: Introdução. Essa ideia só funcionará com telefones ou tablets se a bateria for removível. Observar a polaridade é importante, é claro. Tenha cuidado para não danificar seu dispositivo por descuido. Se você não tiver certeza de sua capacidade de fazer isso
Inversor conectado à rede DIY (não alimenta a rede) Alternativa de UPS: 7 etapas (com fotos)

Inversor DIY Grid Tied (não alimenta a rede) Alternativa de UPS: Este é um post de acompanhamento do meu outro Instructable sobre como fazer um inversor de rede que não realimenta a rede, uma vez que agora é sempre possível fazer isso em certas áreas como um projeto DIY e alguns lugares não permitem a alimentação lá g
