
Índice:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:35.
- Última modificação 2025-01-23 15:03.


Aqui está uma aplicação prática de equações matemáticas complexas.
Esta é de fato uma técnica muito útil que você pode usar para caracterizar componentes, ou mesmo uma antena, em frequências predeterminadas.
Se você está mexendo em eletrônicos, pode estar familiarizado com os resistores e a lei de Ohm. R = V / I Você agora pode se surpreender ao saber que isso é tudo que você precisa resolver para impedâncias complexas também! Todas as impedâncias são essencialmente complexas, ou seja, possuem uma parte Real e uma Imaginária. No caso de um resistor, o imaginário (ou reatância) é 0, correspondentemente, não há diferença de fase entre V e I, portanto, podemos deixá-los de fora.
Um rápido resumo sobre números complexos. Complexo significa simplesmente que o número é composto de duas partes, uma real e uma imaginária. Existem duas maneiras de representar números complexos, por exemplo, na figura acima, um ponto pode ser definido pelos valores Real e Imaginário, como onde as linhas amarela e azul se encontram. Por exemplo, se a linha azul estivesse em 4 no eixo X e 3 no eixo Y, esse número seria 4 + 3i, i indica que essa é a parte imaginária desse número. Outra forma de definir o mesmo ponto seria pelo comprimento (ou amplitude) da linha vermelha e também pelo ângulo que ela faz com a horizontal. No exemplo acima, seria 5 <36,87.
Ou uma linha com comprimento de 5 em um ângulo de 36,87 graus.
Na equação acima de todos os parâmetros, R, V e I podem ser considerados como tendo uma parte imaginária, ao trabalhar com resistores este valor é 0.
Ao trabalhar com indutores ou capacitores, ou quando uma diferença de fase pode ser medida (em graus) entre os sinais, a equação permanece a mesma, mas a parte imaginária do número deve ser incluída. A maioria das calculadoras científicas torna o trabalho com matemática complexa muito fácil. Neste tutorial, vou trabalhar com um exemplo em uma Casio fx-9750GII.
Primeiro, uma recapitulação da equação do divisor de tensão do resistor.
De acordo com a figura -
A tensão em Y é a corrente i multiplicada por R2
i é a tensão X dividida pela soma de R1 e R2
Quando R2 é desconhecido, podemos medir os outros valores, X, Y, R1 e reorganizar a equação para resolver para R2.
Suprimentos
Calculadora científica
Gerador de sinal
Osciloscópio
Etapa 1: configuração

Vamos supor que queremos calcular a indutância do dispositivo em teste (DUT) em 1MHz.
O gerador de sinal é configurado para uma saída senoidal de 5 V a 1 MHz.
Estamos usando resistores de 2k ohm e os canais do osciloscópio são CH1 e CH2
Etapa 2: Osciloscópio

Obtemos as formas de onda conforme mostrado na figura. Uma mudança de fase pode ser vista e medida no osciloscópio para liderar por 130ns. A amplitude é de 3,4V. Observe que o sinal no CH1 deve ser 2,5 V, pois é obtido na saída do divisor de tensão, aqui é mostrado como 5 V para maior clareza, pois este é o valor que também devemos usar em nossos cálculos. ou seja, 5 V é a tensão de entrada para o divisor com o componente desconhecido.
Etapa 3: Calcular a Fase

Em 1 MHz, o período do sinal de entrada é 1us.
130ns dá uma razão de 0,13. Ou 13%. 13% de 360 é 46,6
O sinal de 5 V recebe um ângulo de 0.. já que este é o nosso sinal de entrada e a mudança de fase é relativa a ele.
o sinal de 3,4 V recebe o ângulo de +46,6 (o + significa que está à frente, para um capacitor o ângulo seria negativo).
Etapa 4: na calculadora


Agora, simplesmente inserimos nossos valores medidos na calculadora.
R é 2k
V é 5 (EDIT - V é 5, mais tarde na equação é usado X! O resultado é exatamente o mesmo que i tem X como 5 na minha calculadora)
Y é a nossa tensão medida com o ângulo de fase, este número é inserido como um número complexo, simplesmente especificando o ângulo conforme mostrado na tela da calculadora
Etapa 5: Resolva a Equação

agora a equação
(Y * R) / (X - Y)
é digitado na calculadora, esta é exatamente a mesma equação que usamos para resolver os divisores de tensão do resistor:)
Etapa 6: Valores Calculados


A calculadora deu o resultado
18 + 1872i
O 18 é a parte real da impedância e tem uma indutância de +1872 a 1MHz.
Que funciona para 298uH de acordo com a equação de impedância do indutor.
18 ohms é mais alto do que a resistência que seria medida com um multímetro, isso porque o multímetro mede a resistência em CC. Em 1MHz há efeito pele, no qual a parte interna do condutor é desviado pela corrente e só flui na parte externa do cobre, diminuindo efetivamente a área cruzada do condutor e aumentando sua resistência.
Recomendado:
DIY Como controlar o ângulo do servo motor usando o componente de sequência Visuino: 10 etapas

DIY Como controlar o ângulo do servo motor usando o componente de sequência Visuino: Neste tutorial, usaremos o servo motor e o Arduino UNO, e o Visuino para controlar o ângulo do servo motor usando o componente de sequência. O componente de sequência é perfeito para situações em que queremos acionar vários eventos em sequência no nosso caso servo motor degr
Como escolher a pegada correta do componente: 3 etapas
Como escolher a pegada correta do componente: Uma pegada ou padrão de terreno é o arranjo de almofadas (na tecnologia de montagem em superfície) ou orifícios (na tecnologia de orifícios) usados para anexar fisicamente e conectar eletricamente um componente a uma placa de circuito impresso . O padrão de terra em um circuito
Relógio arco-íris de matemática e física: 3 etapas (com imagens)
Relógio Arco-Íris Matemático-Físico: Um tempo atrás tive a ideia de criar meu próprio relógio Físico / Matemático, então comecei a projetá-lo no Inkscape. A cada hora, de 1 a 12, eu substituí pela fórmula Física / Matemática: 1 - Equação de Euler 2 - Integral 3 - Função trigonométrica 4 - Integral de trigonom
Medindo a impedância usando LTspice: 4 etapas
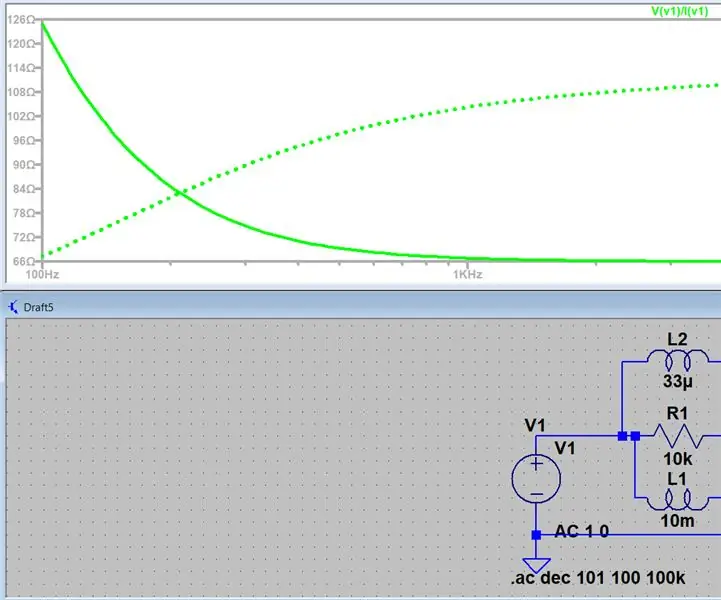
Medindo a impedância usando LTspice: Olá a todos, esta será uma introdução simples para gerar uma varredura CA de um circuito e encontrar a impedância em qualquer ponto. Isso surgiu várias vezes em meus cursos e foi muito difícil para mim encontrar qualquer maneira de fazer isso online então
Matemática rápida 2018: 7 etapas
Quick Math 2018: um jogo que torna o aprendizado divertido novamente
