Plotadora de tambor CNC: 13 etapas (com fotos)

2024 Autor: John Day | [email protected]. Última modificação: 2024-01-30 11:37

Este instrutível descreve uma plotadora A4 / A3 feita de uma seção de tubo plástico, dois motores de passo BYJ-48 e um servo SG-90. Essencialmente, é uma plotadora de base plana enrolada em um tambor.

Um motor gira o tambor enquanto o outro move a cabeça de impressão. O servo é usado para levantar e abaixar a caneta.

Esta plotadora tem uma série de vantagens sobre uma plotadora de mesa tradicional:

• pegada significativamente menor
• requer apenas um trilho guia linear
• simples de construir
• barato

Um intérprete integrado aceita a saída gcode do Inkscape.

A comunicação com o plotter é feita por meio de um link bluetooth.

O plotter é compatível com o CNC Graphics Tablet descrito em minha https://www.instructables.com/id/CNC-Graphics-Table …

Embora não seja um instrumento de precisão, a exatidão deste plotter é satisfatória para o propósito pretendido de transferir contornos de aquarela para o papel.

Etapa 1: O circuito

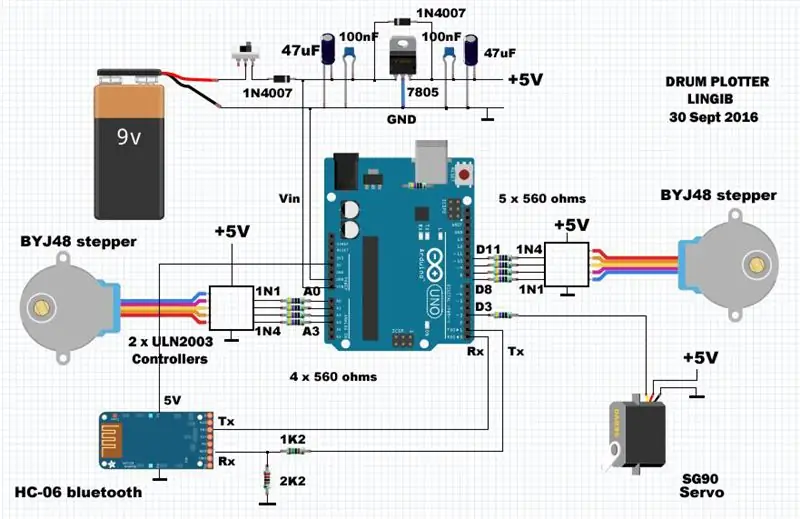
O circuito compreende um microcontrolador Arduino UNO R3 e uma blindagem personalizada na qual os componentes discretos são montados. A alimentação é aplicada por meio de um regulador externo de 5 volts e 1 ampere. A corrente média está em torno de 500mA.

Os motores de passo BYJ-48 são conectados ao PORTB (pinos D8, D9, D10, D11) e PORTC (pinos A0, A1, A2, A3). O servo pen-lift SG-90 é conectado ao pino D3.

Os resistores de 560 ohms, que podem ser omitidos, fornecem uma medida de proteção contra curto-circuito para o arduino caso algo dê errado. Eles também facilitam a fiação da blindagem, pois atuam como "jumpers" nos trilhos de alimentação.

Os resistores 1k2 e 2K2 evitam danos ao módulo bluetooth HC-06 [1] diminuindo a saída de 5 volts do arduino para 3,3 volts.

[1] Desconecte o módulo de bluetooth HC-06 ao enviar o código para o arduino através da porta USB. Isso evitará conflitos de porta serial.

Etapa 2: A unidade linear

O acionamento linear é feito de uma barra de alumínio de 3 mm x 32 mm, uma tira de folha de alumínio e quatro pequenas polias de rolamento de esferas.

O alumínio está disponível na maioria das lojas de ferragens. As polias com ranhura em U U624ZZ 4x13x7mm estão disponíveis em

Ferramentas manuais simples são tudo o que você precisa. Corte a barra de alumínio de acordo com as dimensões da plotadora.

O conjunto do motor

Monte o motor de passo BJY-48 através da barra em uma extremidade e conecte um dente GT2 20, furo de 5 mm, polia ao eixo do motor. Agora monte outra polia GT2 na outra extremidade da barra de forma que a polia possa girar livremente. Usei um espaçador tubular (rádio) de 5 mm de diâmetro e um parafuso de 3 mm para fazer isso.

Agora enrole um pedaço de correia dentada GT2 em torno das polias. Una as pontas da correia dentada por meio de meia torção de modo que os dentes se intercalem e fixem com uma braçadeira.

Por fim, prenda o conjunto do carro à correia dentada com uma braçadeira.

A carruagem montada

O conjunto do carro é feito de uma tira de folha de alumínio [1] na qual as polias U624ZZ são aparafusadas. Se necessário, use uma arruela de 4 mm para afastar as polias da folha de alumínio.

As polias, que têm uma ranhura de 4 mm, estendem-se na parte superior e inferior da barra de alumínio de forma que não haja movimento vertical, embora a tira de alumínio se mova livremente para a esquerda e para a direita.

Para garantir que o carro funcione livremente, monte primeiro as duas polias superiores e, em seguida, com as polias apoiadas na barra, marque as posições das duas polias inferiores. Os orifícios para essas duas polias agora podem ser perfurados. Use uma pequena broca "piloto" primeiro para evitar que a broca maior de 4 mm se desvie.

Antes de dobrar a tira de alumínio em um "U", faça um orifício na parte superior e inferior para se adequar ao diâmetro da caneta. Agora complete as curvas.

Prenda a correia dentada ao conjunto do carro por meio de uma braçadeira e parafuso de 3 mm entre as duas polias superiores.

O conjunto de caneta-elevador

Conecte um servo SG-90 à parte superior do conjunto do carro usando uma ou duas abraçadeiras.

Solte a caneta nos dois orifícios que você fez. Certifique-se de que a caneta desliza para cima e para baixo livremente.

Prenda um "colar" em sua caneta de forma que a caneta fique apenas fora do tambor quando o servo estiver na posição de caneta para cima.

[1] O alumínio pode ser cortado marcando ambos os lados da folha com uma faca afiada (cortador de caixa) e, em seguida, flexionando o corte sobre a borda de uma mesa. Alguns movimentos e a folha irá se quebrar, deixando uma quebra direta. Ao contrário dos recortes de estanho, este método não torce o alumínio.

Etapa 3: o tambor

O tambor é composto por uma seção de tubo de plástico com duas tampas de madeira [1].

Use uma bússola, definida para o raio interno de seu tubo, para desenhar os contornos do plugue final. Agora corte ao redor de cada contorno usando uma serra de lâmina fina ("coping", "traste") e ajuste cada plugue com a ajuda de uma lima para madeira. Aperte os plugues finais usando pequenos parafusos de madeira rebatidos.

Um parafuso de engenharia de 6 mm no centro de cada tampão forma o eixo.

Dimensões do tambor

As dimensões do cilindro são determinadas pelo tamanho do papel. Um diâmetro de cilindro de 100 mm suporta retrato A4 e paisagem A3. Um diâmetro de cilindro de 80 mm suportará apenas paisagem A4. Use o menor diâmetro de tambor possível para reduzir a inércia … os motores BYJ-48 são apenas pequenos.

Um cilindro de diâmetro de 90 mm é ideal para papel A4 retrato e A3 paisagem, pois as bordas opostas, quando enroladas em torno do cilindro, se sobrepõem em aproximadamente 10 mm, o que significa que você só tem uma costura para colar no lugar.

Girando o tambor

Cada eixo passa por um suporte de extremidade de alumínio de forma que o tambor possa girar livremente. A flutuação da extremidade é evitada por meio de um GT-2, 20 dentes, furo de 6 mm, polia presa ao eixo em uma extremidade. Uma correia dentada GT-2 contínua conecta o motor de passo com engrenagem BJY-48 ao tambor. O motor requer uma polia com diâmetro de 5 mm.

[1] Tampões de plástico estão disponíveis para a maioria dos diâmetros de tubos, mas foram rejeitados porque se encaixam no tubo, e não no interior, e o plástico tende a flexionar. Eles provavelmente estariam bem se um eixo contínuo fosse usado em vez dos parafusos … mas então você precisa de algum método de fixação do eixo aos plugues finais.

Etapa 4: dicas de construção

Certifique-se de que a caneta se desloca ao longo do centro do tambor. Isso pode ser conseguido cortando os cantos dos suportes de madeira. Se a caneta estiver descentralizada, ela tenderá a deslizar para baixo na lateral do cilindro.

A perfuração precisa dos dois orifícios da caneta é importante. Qualquer oscilação na guia da caneta ou no conjunto do carro causará oscilações ao longo do eixo X.

Não aperte demais as correias dentadas GT-2 … elas só precisam estar bem esticadas. Os motores de passo BYJ-48 não têm muito torque.

Os motores de passo BJY-48 geralmente exibem pequenas quantidades de folga que é insignificante ao longo do eixo X, mas é uma preocupação quando se trata do eixo Y. A razão para isso é que uma rotação do motor do eixo Y equivale a uma rotação do tambor, enquanto o carro da caneta requer muitas voltas do motor do eixo X para percorrer o comprimento do tambor. Qualquer folga do eixo Y pode ser eliminada mantendo um torque constante no tambor. Um método simples é prender um pequeno peso a um fio de náilon enrolado no tambor.

Etapa 5: Algoritmo de desenho de linha de Bresenham

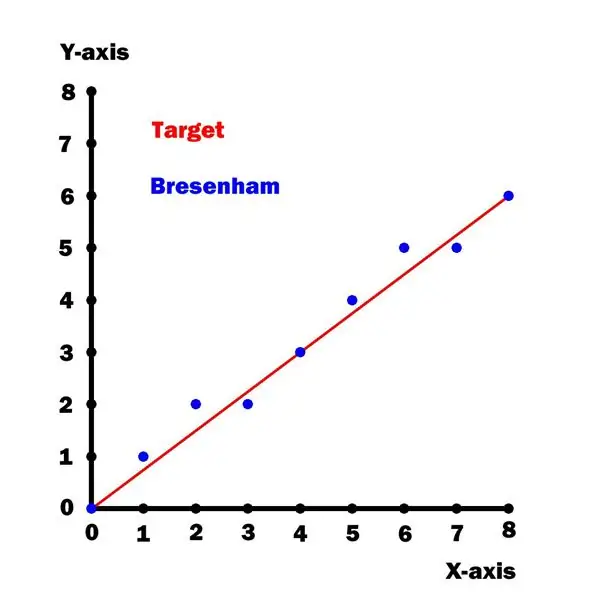
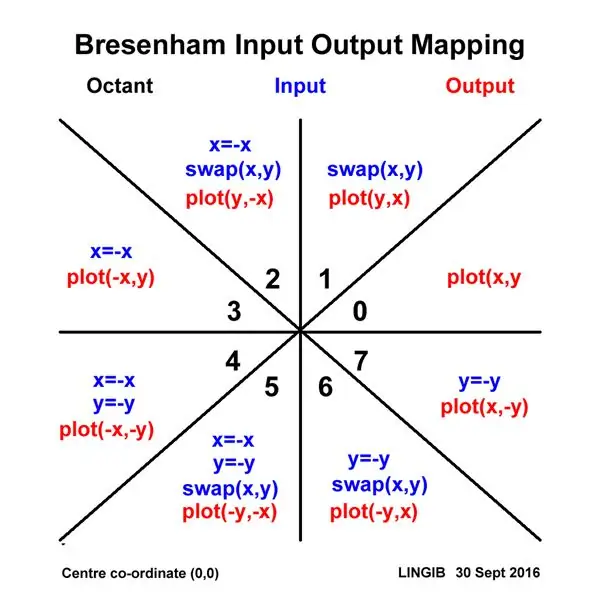
Este plotter usa uma versão otimizada [1] do algoritmo de desenho de linha de Bresenham. Infelizmente, este algoritmo só é válido para inclinações de linha menores ou iguais a 45 graus (ou seja, um octante de um círculo).

Para contornar essa limitação, "mapeio" todas as entradas XY para o primeiro "octante" e, em seguida, "desmapea" quando chegar a hora de plotar. As funções de mapeamento de entrada e saída para conseguir isso são mostradas no diagrama acima.

Derivação

O restante desta etapa pode ser omitido se você estiver familiarizado com o algoritmo de Bresenham.

Vamos desenhar uma linha de (0, 0) a (x1, y1) onde:

• x1 = 8 = distância horizontal
• y1 = 6 = distância vertical

A equação para uma linha reta passando pela origem (0, 0) é dada pela equação y = m * x onde:

m = y1 / x1 = 6/8 = 0,75 = inclinação

Algoritmo Simples

Um algoritmo simples para traçar esta linha é:

• int x1 = 8;
• int y1 = 6;
• float m = y1 / x1;
• plot (0, 0);
• para (int x = 1; x <= x1; x ++) {
• int y = redondo (m * x);
• plot (x, y);
• }

Tabela 1: Algoritmo Simples

x	m	m * x	y
0	0.75	0	0
1	0.75	0.75	1
2	0.75	1.5	2
3	0.75	2.25	2
4	0.75	3	3
5	0.75	3.75	4
6	0.75	4.5	5
7	0.75	5.25	5
8	0.75	6	6

Existem dois problemas com este algoritmo simples:

• o loop principal contém uma multiplicação que é lenta
• ele usa números de ponto flutuante que também são lentos

Um gráfico de y versus x para esta linha é mostrado acima.

Algoritmo de Bresenham

Bresenham introduziu o conceito de um termo de erro 'e' que é inicializado com zero. Ele percebeu que os valores de m * x mostrados na tabela 1 podem ser obtidos pela adição sucessiva de 'm' a 'e'. Ele percebeu ainda que y só é incrementado se a parte fracionária de m * x for maior que 0,5. Para manter sua comparação dentro do intervalo 0 <= 0,5 <= 1, ele subtrai 1 de 'e' sempre que y é incrementado.

• int x1 = 8;
• int y1 = 6;
• float m = y1 / x1;
• int y = 0;
• float e = 0;
• plot (0, 0);
• para (int x = 1; x <= x1; x ++) {
• e + = m;
• if (e> = 0,5) {
• e - = 1;
• y ++;
• }
• plot (x, y);
• }

Tabela 2: Algoritmo de Bresenham

x	m	e	e-1	y
0	0.75	0	0	0
1	0.75	0.75	-0.25	1
2	0.75	0.5	-0.5	2
3	0.75	0.25		2
4	0.75	1	0	3
5	0.75	0.75	-0.25	4
6	0.75	0.5	-0.5	5
7	0.75	0.25		5
8	0.75	1	0	6

Se você examinar o algoritmo e a tabela 2, você observará isso;

• o loop principal só usa adição e subtração … não há multiplicação
• o padrão para y é o mesmo da tabela 1.

Mas ainda estamos usando números de ponto flutuante … vamos consertar isso.

Algoritmo de Bresenham (otimizado)

O algoritmo de ponto flutuante de Bresenham pode ser convertido para uma forma inteira se escalarmos 'm' e 'e' em 2 * x1, caso em que m = (y1 / x1) * 2 * x1 = 2 * y1

Além de escalar 'm' e 'e', o algoritmo é semelhante ao acima, exceto:

• adicionamos 2 * y1 a 'e' cada vez que incrementamos 'x"
• incrementamos y se e for igual ou maior que x1.
• subtraímos 2 * x1 de 'e' em vez de 1
• x1 é usado para a comparação em vez de 0,5

A velocidade do algoritmo pode ser aumentada ainda mais se o loop usar zero para o teste. Para fazer isso, precisamos adicionar um deslocamento ao termo de erro 'e'.

• int x1 = 8;
• int y1 = 6;
• int m = (y1 << 1); // constante: declive dimensionado por 2 * x1
• int E = (x1 << 1); // constante: 2 * x1 para uso em loop
• int e = -x1; // deslocamento de -E / 2: teste agora feito em zero
• plot (0, 0);
• int y = 0;
• para (x = 1; x <= x1; x ++) {
• e + = m;
• if (e> = x1) {
• e - = E
• y ++;
• }
• plot (x, y);
• }

Tabela 3: Algoritmo de Bresenham (otimizado)

x	m	E	e	e - E	y
0	12	16	-8		0
1	12	16	4	-12	1
2	12	16	0	-16	2
3	12	16	-4		2
4	12	16	8	-8	3
5	12	16	4	-12	4
6	12	16	0	-16	5
7	12	16	-4		5
8	12	16	8	-8	6

Mais uma vez, o padrão para y é o mesmo das outras tabelas. É interessante notar que a tabela 3 contém apenas inteiros e que a razão de m / E = 12/16 = 0,75 que é a inclinação 'm' da reta.

Este algoritmo é extremamente rápido, pois o loop principal envolve apenas adição, subtração e uma comparação com zero. A multiplicação não é usada exceto quando inicializamos os valores de 'E' e 'm' usando um "deslocamento para a esquerda" para dobrar os valores de x1 e y1.

[1] Esta versão otimizada do algoritmo de Bresenham é de um artigo "Bresenham Line and Circle Drawing", copyright © 1994-2006, W Randolph Franklin (WRF). Seu material pode ser usado para pesquisa e educação sem fins lucrativos, desde que você dê o crédito a ele e faça um link para sua página inicial,

Etapa 6: O Código

Baixe o arquivo anexado em uma pasta com o mesmo nome e carregue-o na plotadora usando o seu IDE arduino (ambiente de desenvolvimento integrado).

Desconecte o módulo HC-06 bluetoorh antes de tentar o upload. Isso é necessário para evitar um conflito de porta serial com o cabo USB.

Código de Terceiros

Além do código.ino acima, você precisará dos seguintes pacotes de software que são gratuitos / de doação:

• Teraterm que está disponível em
• Inkscape que está disponível em

As instruções para instalar e usar cada um dos pacotes de terceiros acima podem ser encontradas em meu artigo

Etapa 7: Menu

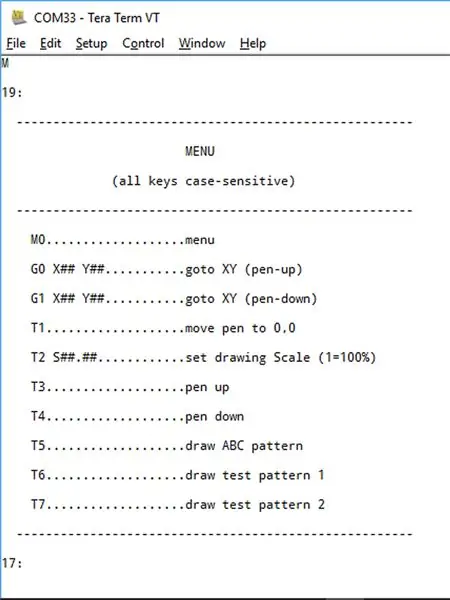
Faça uma conexão bluetooth com sua plotadora usando "Teraterm".

Ative o "caps lock", pois todos os comandos estão em maiúsculas.

Digite a letra 'M' e um menu deve aparecer como mostrado acima.

O menu é razoavelmente autoexplicativo:

• M (ou M0) abre o menu
• G0 permite que você envie a caneta para uma coordenada XY específica com a caneta levantada.
• G1 permite que você envie a caneta para uma coordenada XY específica com a caneta abaixada.
• T1 permite que você posicione sua caneta sobre sua coordenada 0, 0. Digite 'E' para sair.
• T2 permite dimensionar seu desenho. Por exemplo, "T2 S2.5" dimensionará seu desenho em 250%. A escala padrão é 100%
• T3 e T4 permitem que você levante ou abaixe a caneta.
• T5 desenha um padrão de teste "ABC".
• T6 desenha um "alvo".
• T7 desenha um conjunto de linhas radiais, cujo objetivo é verificar se o algoritmo de Bresenham está funcionando em cada um dos oito "octantes"

Notas:

• todos os movimentos da caneta usam a escala de desenho definida usando a opção de menu T2
• os números "17:" e "19:" são os códigos de handshake do terminal "Xon" e "Xoff" do interpretador arduino.

Etapa 8: Calibração

Os valores para X_STEPS_PER_MM e Y_STEPS_PER_MM são para um cilindro de 90 mm de diâmetro.

Os valores para outros diâmetros de tambor podem ser calculados usando as seguintes relações:

• a circunferência do tambor é PI * diâmetro
• 2048 etapas equivalem a uma revolução de cada eixo do motor
• uma revolução de uma polia GT-2 equivale a um movimento linear de 40 milímetros de uma correia dentada

Outro método é inserir os seguintes comandos,

• G1 X0 Y100
• G1 X100 Y100

em seguida, meça o comprimento das linhas resultantes e "dimensione" os valores para X-STEPS_PER_MM e Y_STEPS_PER_MM

Etapa 9: pré-processamento do Gcode

Este plotter requer apenas quatro dos gcodes do Inkscape (viz: G0, G1, G2, G3). O código será executado significativamente mais rápido se removermos todos os gcodes e comentários desnecessários.

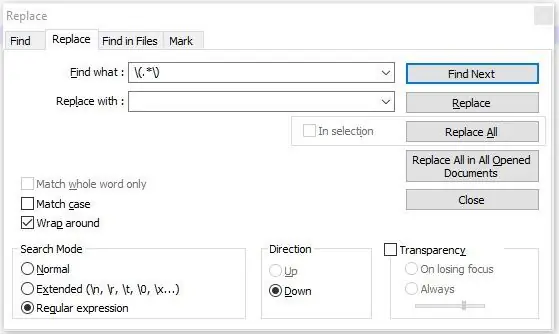
Para fazer isso, você precisa de uma cópia do "Notepad ++". Este editor de texto gratuito contém um mecanismo de pesquisa de "expressão regular" para localizar e remover texto indesejado. O Notepad ++ está disponível em

Abra o arquivo a ser modificado com o Notepad ++ e posicione o cursor na parte superior do arquivo.

Selecione "Exibir / Mostrar símbolo / Todos os caracteres" seguido de "Pesquisar / Substituir …" na barra de menu superior.

Clique na caixa de seleção "Expressão regular" (veja a 1ª imagem) e insira cada uma das seguintes sequências de código na caixa de pesquisa.

Clique em "Substituir tudo" após cada entrada:

• %
• (.*)
• ^ M. * $
• Z. * $

As expressões regulares acima removem todos os símbolos%, todos os comentários mostrados entre colchetes, todos os códigos M, todos os códigos Z e os códigos que se seguem.

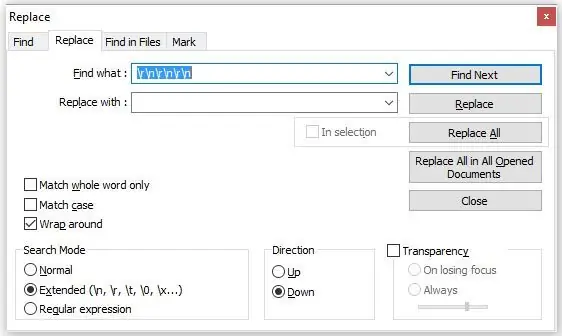
Agora clique na caixa de seleção "Expressão estendida" (veja a 2ª imagem) e insira a seguinte sequência de código:

r / n / r / n / r / n

Esta expressão remove os retornos de carro indesejados e avanços de linha criados pela primeira sequência.

Salve seu arquivo com um nome diferente usando "Salvar como".

Feito.

Etapa 10: Resultados

Este plotter foi construído como "prova de conceito" e nunca teve a intenção de ser perfeito. Dito isto, os resultados não são tão maus. Eles definitivamente atendem ao meu objetivo de design de transferir contornos de aquarela para o papel.

As três primeiras imagens são os padrões de teste integrados T5, T6 e T7, respectivamente.

O "Hello World!" o padrão foi enviado ao plotter via bluetooth. Uma cópia "pré-processada" deste arquivo está anexada.

Etapa 11: atualização do código

O código desta plotadora foi atualizado para Drum_Plotter_V2.ino.

As alterações do Drum_Plotter.ino original incluem:

• posicionamento mais suave da caneta
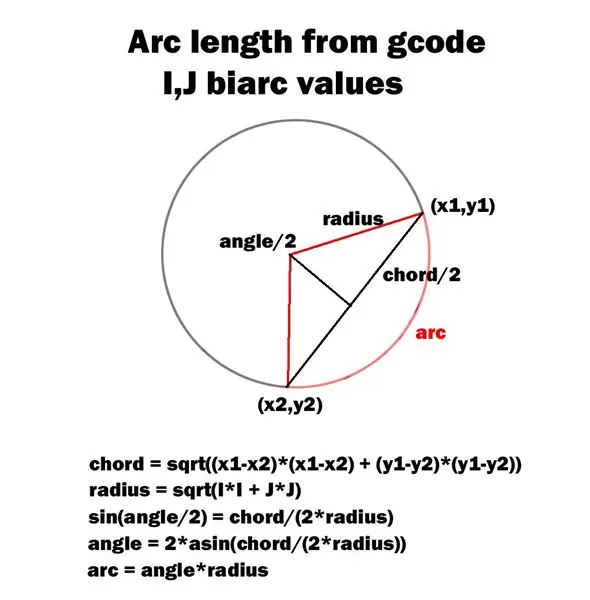
• agora reconhece instruções G02 gcode (arcos no sentido horário)
• agora reconhece as instruções G03 gcode (arcos no sentido anti-horário)

O diagrama anexo descreve meu método para calcular o ângulo do arco.

Etapa 12: Drum_plotter_v3.ino

Uma atualização de código para "CNC Drum Plotter" está anexada.

"drum_plotter_v3.ino" corrige um pequeno bug que afetava a precisão da plotadora.

Histórico de mudanças

Versão 2:

Curvas bi-arco adicionadas

Versão 3:

As funções a seguir foram reescritas para resolver um pequeno bug que afetou a precisão da plotadora.

• (int) substituído por round () na função move_to ().
• algoritmo de busca "octante" da função draw_line () melhorado
• O interpretador agora usa funções de string em vez de ponteiros, o que simplifica o design. Por exemplo, agora podemos pesquisar "MENU" em vez de procurar a letra 'M' e extrair o número inteiro que se segue. Isso permite que você personalize a plotadora com seus próprios comandos.

Etapa 13: Drum_plotter_plotter_v4.ino

16 de janeiro de 2017:

O código para este plotter de tambor foi otimizado ainda mais. Recursos adicionais foram adicionados.

As mudanças incluem:

• algoritmo draw_line () mais rápido
• correspondente à função move_to ()
• contadores de passos
• pequena correção de bug

Para obter mais detalhes, leia os comentários em "drum_plotter_v4.ino" em anexo.

Clique aqui para ver meus outros instructables.