Como criar uma cúpula geodésica estilo Temcor no Autodesk Inventor: 8 etapas

2024 Autor: John Day | [email protected]. Última modificação: 2024-01-30 11:38

Este tutorial mostrará como criar uma cúpula no estilo Temcor usando apenas um pouco de matemática.

A maioria das informações neste tutorial foi obtida da engenharia reversa do método de subdivisão da antiga Estação Amundsen-Scott no Pólo Sul de TaffGoch, portanto, um grande obrigado a ele!

Uma grande vantagem das cúpulas Temcor é sua baixa contagem única de escoras - ela aumenta aritmeticamente com frequência, não diferente da grade geodésica triacontahédrica regular de Duncan Stuart (Método 3 *), mas o resultado parece muito mais agradável.

Para simplificar, a frequência da cúpula que estamos fazendo é 14, portanto, os fatores de acordes podem ser verificados em comparação com o modelo Temcor de TaffGoch.

O.ipt do Inventor 2016 está incluído no final do tutorial.

*ATUALIZAR*

Descrevi o Método 4 como a grade geodésica triacontahédrica regular de Duncan Stuart, mas não é. O método foi inventado por Christopher Kitrick, que, em seu artigo de 1985, "Geodesic Domes", descreveu sua construção. Além disso, em seu artigo de 1990, "Uma Abordagem Unificada para Cúpulas Geodésicas de Classe I, II e III", ele descreve 8 outros métodos, um deles sendo o Método 3 de Duncan Stuart, o outro seu próprio "Método 4" e, surpreendentemente o suficiente, um método análogo ao de Temcor, que ele chama de "Método aa" (a etapa 7 mostra como Temcor modificou o "Método aa"). Em um futuro instrutível, descreverei a construção dos métodos descritos neste último artigo.

Etapa 1: Parâmetros do usuário

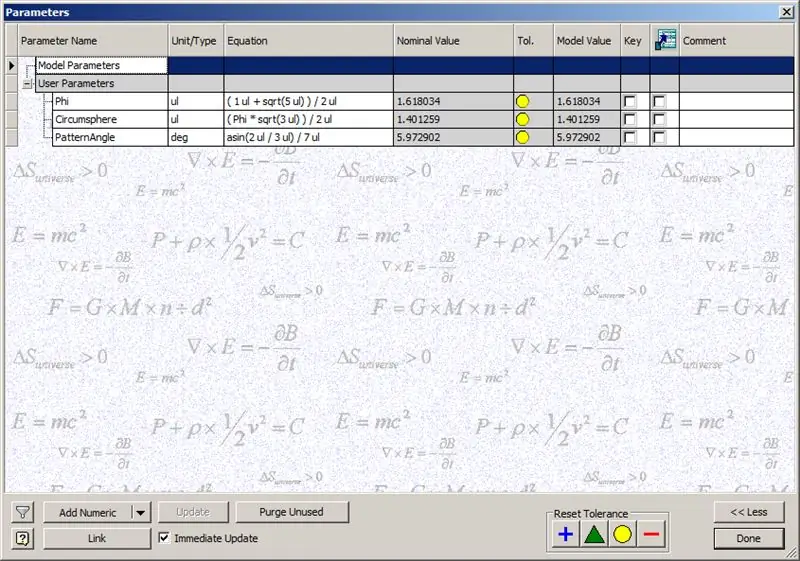
Antes de começarmos a construir a cúpula, insira os parâmetros mostrados:

Phi - a proporção áurea. Definido como ((1 + √5 /) 2

Circunsfera - esta é a circunsfera de um dodecaedro, definida como ((Phi * √3) / 2)

PatternAngle - Este é o ângulo central de um dodecaedro. Como a frequência da nossa cúpula é 14, dividimos esse ângulo central pela metade da frequência, neste caso, 7.

Etapa 2: esboçar um retângulo dourado

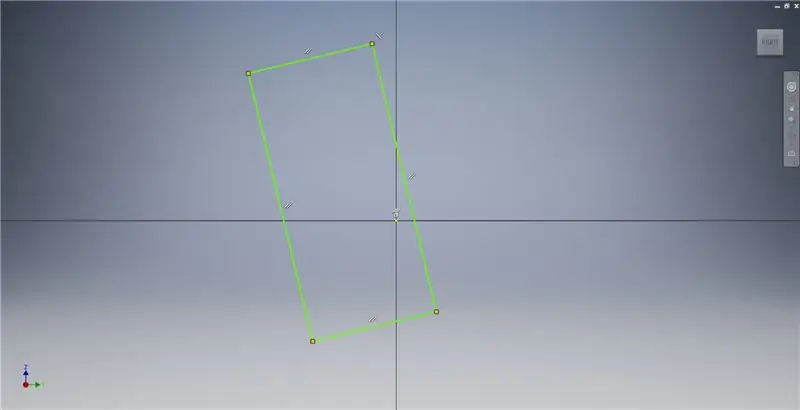
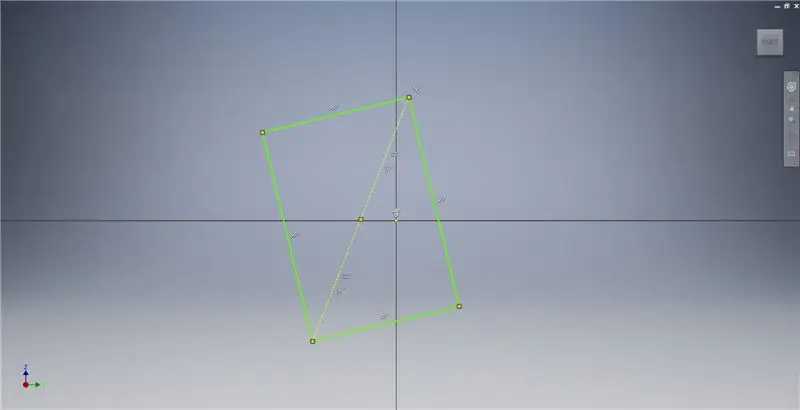
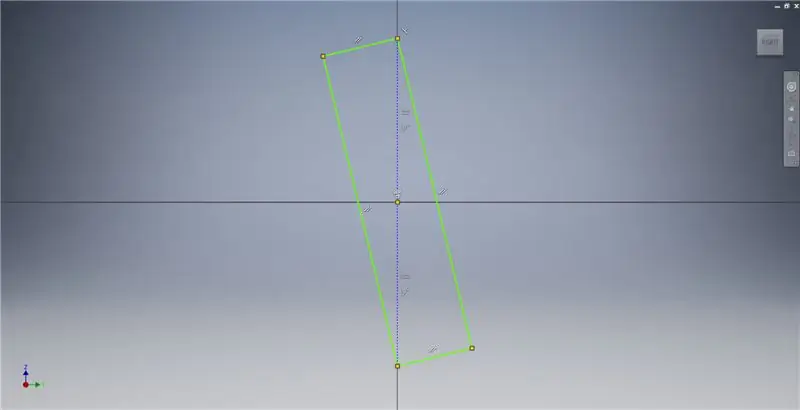
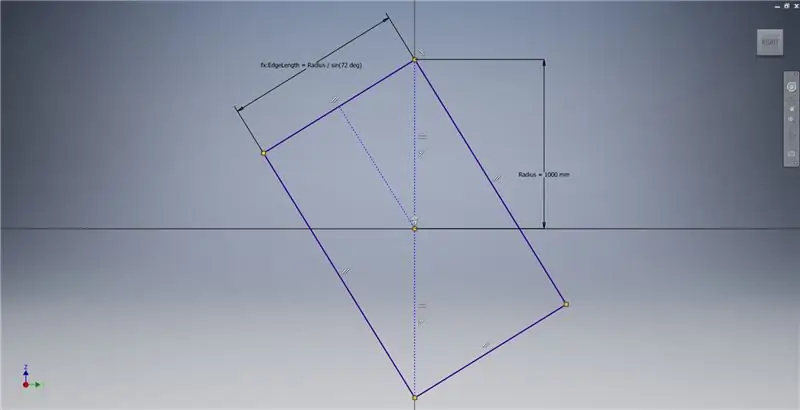
Comece um esboço no plano YZ e, em seguida, crie um retângulo de três pontos como mostrado, referindo-se às notas da imagem para obter informações adicionais que descrevem a criação de um retângulo dourado.

Etapa 3: Criação de um retângulo dourado²

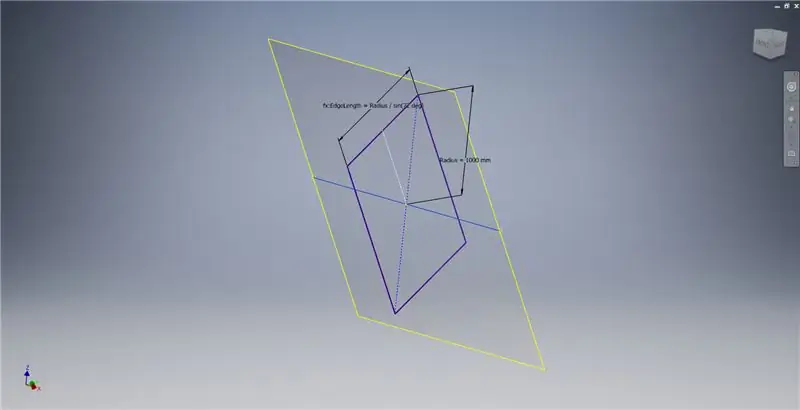
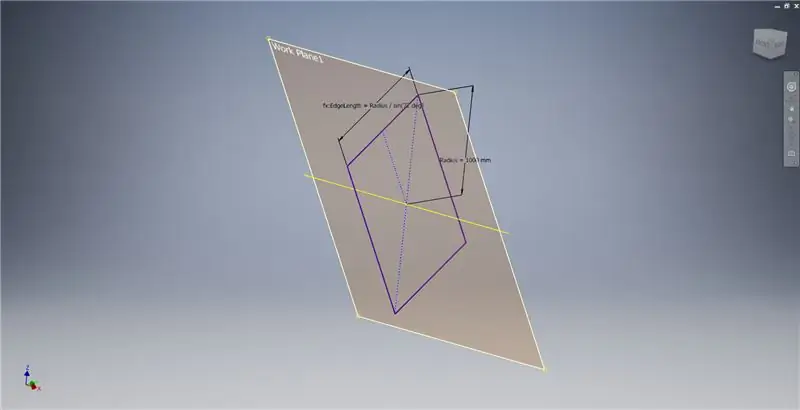
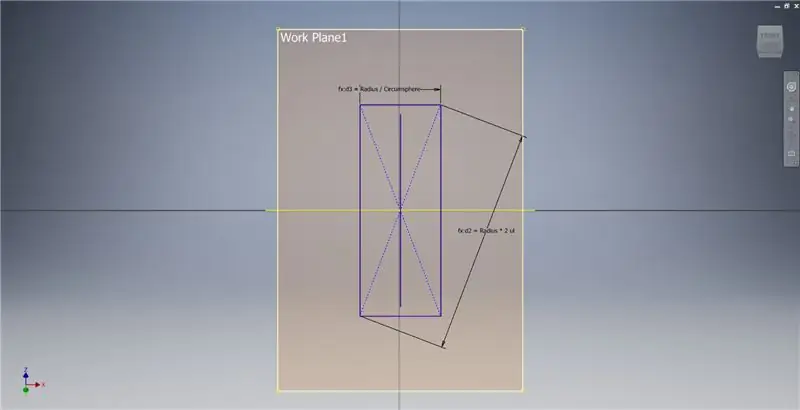
Crie um plano de trabalho usando o eixo X e a linha destacada na primeira imagem e, a seguir, inicie outro esboço neste plano de trabalho. Construa um retângulo de ponto central começando da origem e, a seguir, dimensione o retângulo como mostrado na terceira imagem.

Etapa 4: Criando o Triângulo Triácono 2v

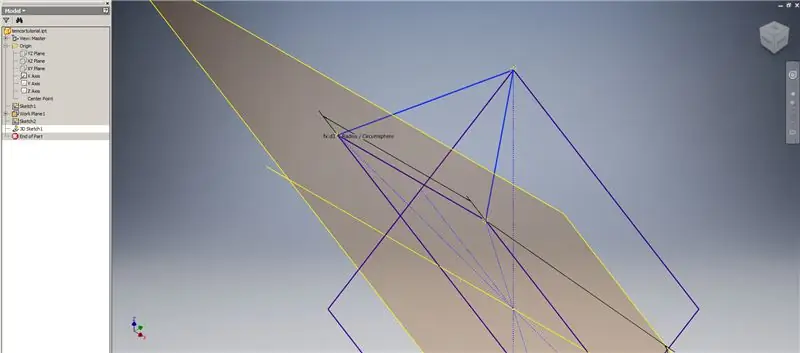
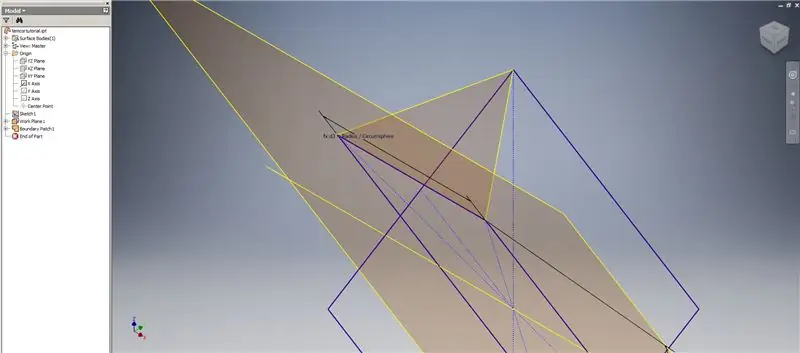
Agora que temos toda a geometria de que precisamos, forme o patch de limite na segunda imagem usando o método de sua preferência. Eu escolhi fazer um esboço 3D, mas esboçar em outro plano de trabalho funcionaria tão bem.

Etapa 5: Criando os planos de interseção

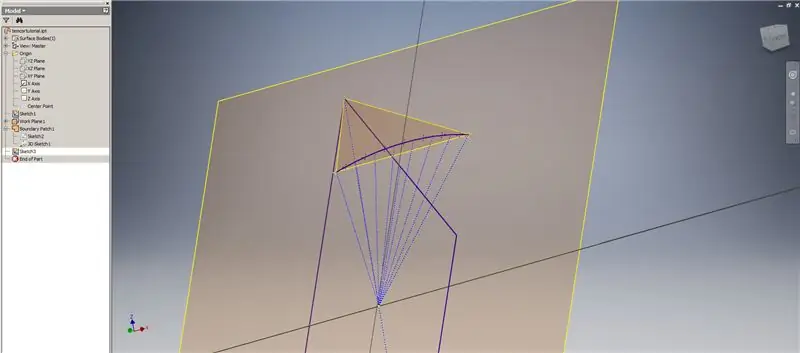
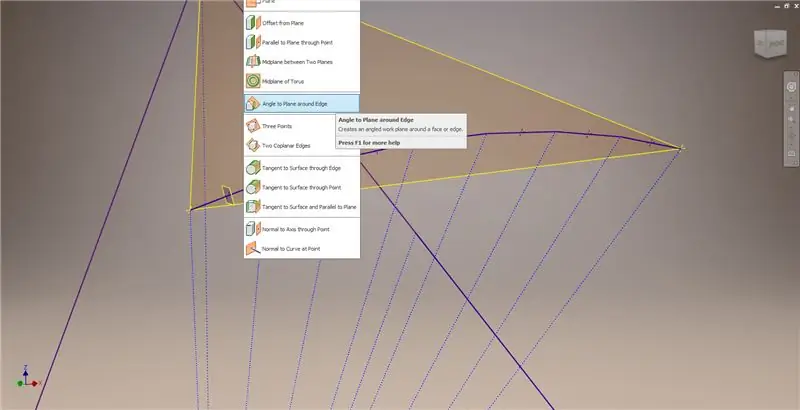
Comece outro esboço no primeiro plano de trabalho ("Plano de trabalho 1") que você criou, projete os cantos do Retângulo Dourado² e conecte esses pontos e a origem para formar o ângulo central do triacontaedro 2v. Divida-o pela metade da frequência da cúpula, como se você estivesse iniciando uma quebra do Método 2. Coloque pontos nos pontos médios dos acordes.

Saia do esboço e crie um plano usando uma das cordas e seu ponto médio, como mostrado na segunda imagem. Em seguida, crie outro plano de trabalho usando "Angle to Plane around Edge". Selecione o plano de trabalho 1 e uma das linhas de construção mostradas na imagem central direita e inferior esquerda. Aceite o ângulo padrão de 90 graus, caso contrário, o resto da subdivisão não pareceria correto. Repita o processo usando o resto dos acordes e linhas de construção para obter o resultado na imagem inferior direita.

Etapa 6: Criando as curvas de interseção e formando a subdivisão

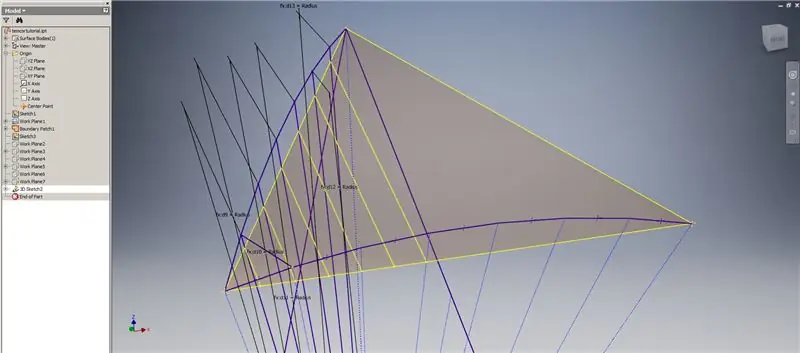
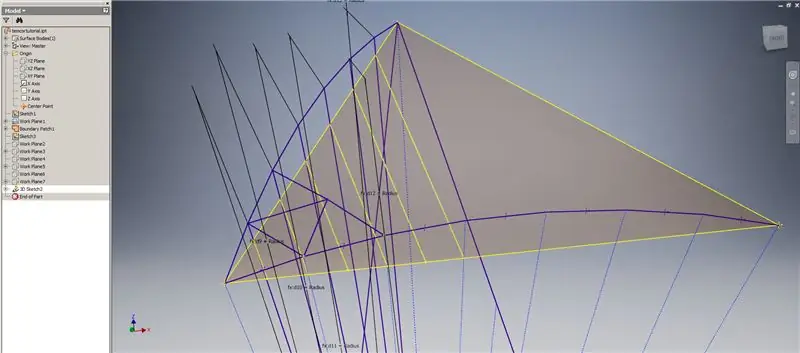
Inicie um esboço 3D e, a seguir, crie curvas de interseção usando os planos de trabalho que você acabou de criar e o retalho de limite, formando as linhas mostradas na imagem superior.

Desenhe linhas coincidentes com os pontos finais das curvas de interseção, conforme mostrado na Imagem 2. Faça todas iguais ao raio da cúpula. Desenhe as cordas unindo as linhas que se encontram nas curvas de interseção. Conecte qualquer geometria que pareça próxima o suficiente para formar um triângulo da subdivisão. Consulte as próximas 10 imagens para saber quais acordes devem ser espelhados nos planos de trabalho de interseção - eles podem explicar isso melhor do que meras palavras.

Etapa 7: Concluindo a cúpula

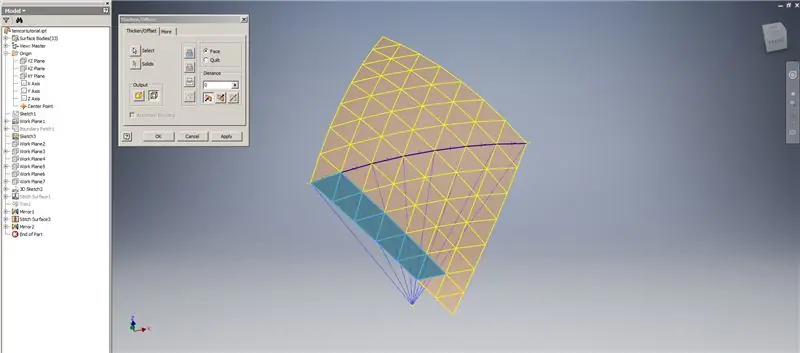
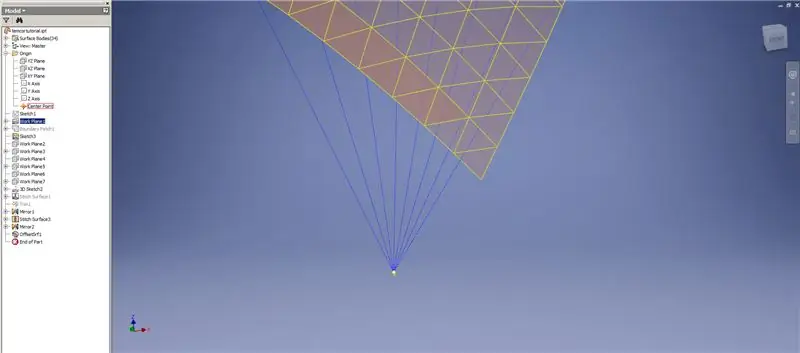
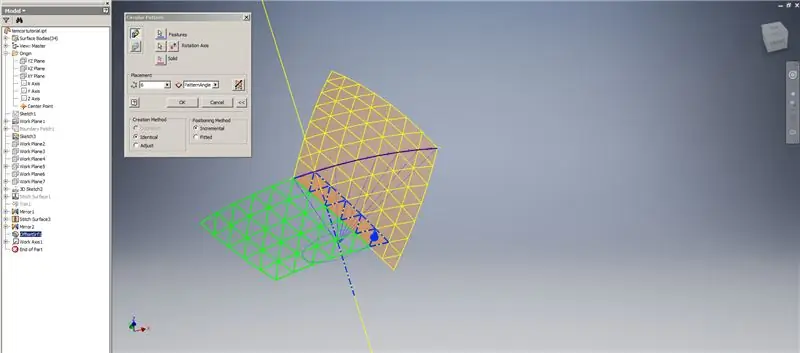
Crie um engrossar / deslocamento das linhas inferiores, omitindo as duas últimas linhas de triângulos. Padronize o novo OffsetSrf 6 vezes ou ((Frequency = 14) / 2) -1. Oculte o OffsetSrf, costure as superfícies padronizadas e espelhe a superfície costurada com o plano YZ. Crie planos de trabalho apoiados nos vértices do triângulo superior, como mostrado na Imagem 6. Apare as superfícies costuradas e espelhadas usando esses novos planos de trabalho e, a seguir, costure as superfícies restantes. Padronize esta última superfície ao longo do eixo Z, em seguida, costure essas superfícies finais e pronto!

Etapa 8: Verificação de acordes

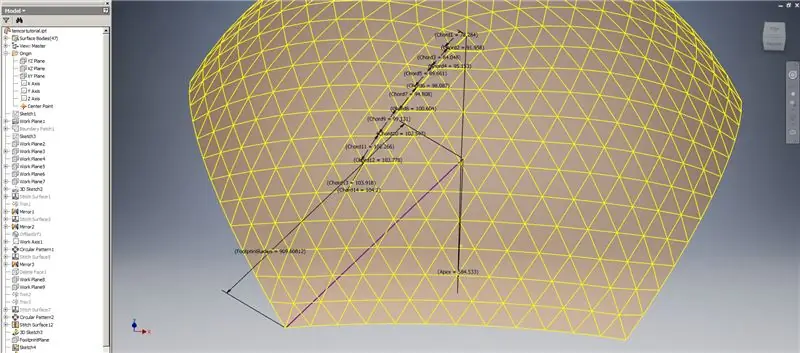
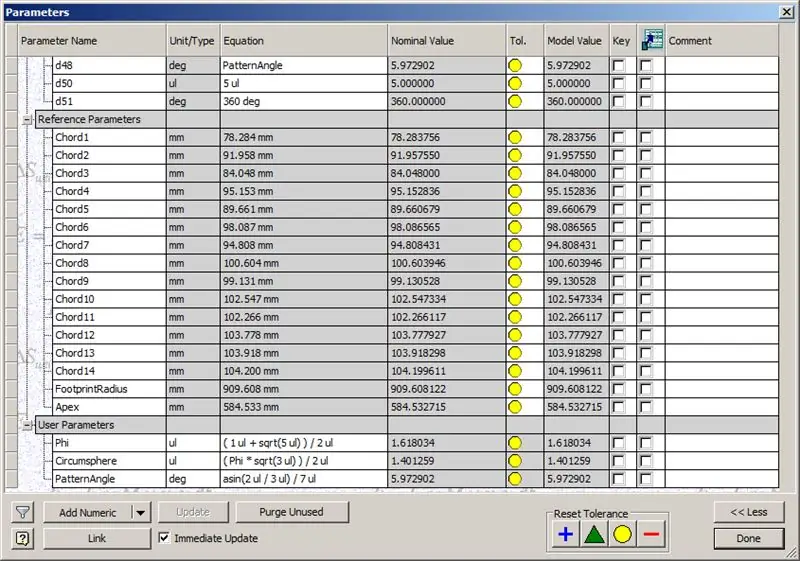
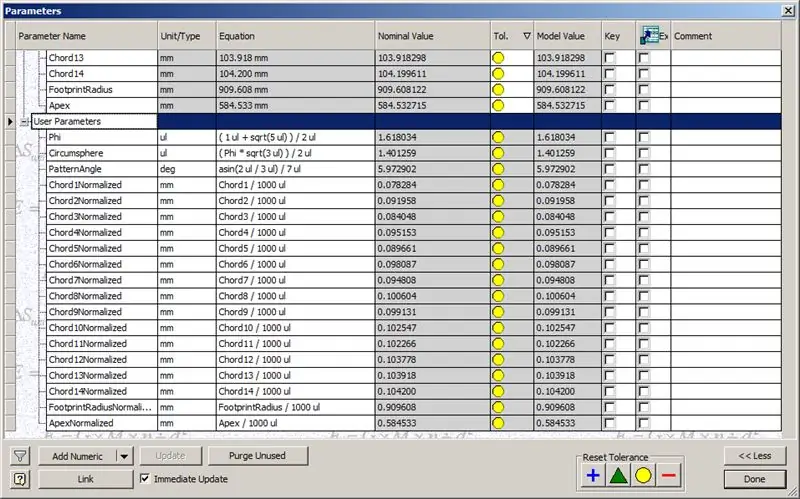
Então, nossa cúpula está pronta, mas vamos ver se os números combinam com o modelo de TaffGoch:

Indo pelos parâmetros de referência, parece que eles são uma combinação perfeita!

Dividindo os comprimentos de corda por 1000, podemos ver claramente uma correspondência perfeita com os fatores de corda do modelo de TaffGoch, bem como o raio da pegada e fatores de ápice.