Robô de autoequilíbrio usando algoritmo PID (STM MC): 9 etapas

2024 Autor: John Day | [email protected]. Última modificação: 2024-01-30 11:38

Recentemente, muito trabalho foi feito no autobalanceamento de objetos. O conceito de auto-equilíbrio começou com o equilíbrio do pêndulo invertido. Esse conceito se estendeu também ao design de aeronaves. Neste projeto, desenhamos um pequeno modelo de robô com autobalanceamento utilizando o Algoritmo PID (Proporcional, Integral, Derivativo). Desde então, esse método é a nova cara dos sistemas de controle de processos industriais. Este relatório analisa os métodos envolvidos no autobalanceamento de objetos. Este projeto foi realizado como um projeto semestral para entender a correlação do PID na eficiência de vários processos industriais. Aqui, nos concentramos apenas em fornecer uma breve revisão sobre a eficácia e a aplicação do controle PID. Este artigo foi desenvolvido fornecendo uma breve introdução aos sistemas de controle e terminologias relacionadas, além das motivações para o projeto. Experimentação e observações foram feitas, méritos e deméritos descritos com finalização nas melhorias futuras. Um modelo de robô com autobalanceamento foi desenvolvido para entender a eficácia do PID no mundo dos sistemas de controle. Passando por alguns testes e experimentos rigorosos, os méritos e deméritos do sistema de controle PID foram descobertos. Verificou-se que apesar das muitas vantagens do controle PID em relação aos métodos anteriores, este sistema ainda requer muitas melhorias. Espera-se que o leitor tenha uma boa compreensão da importância do autobalanceamento, da eficácia e das deficiências do controle PID

Etapa 1: Introdução

Com o advento dos computadores e a industrialização de processos, ao longo da história do homem, sempre houve pesquisas para desenvolver maneiras de refinar processos e, mais importante, controlá-los usando máquinas de forma autônoma. O objetivo é reduzir o envolvimento do homem nesses processos, reduzindo assim o erro nesses processos. Assim, o Campo de”Engenharia de Sistema de Controle” foi desenvolvido. A Engenharia do Sistema de Controle pode ser definida como o uso de vários métodos para controlar o funcionamento de um processo ou a manutenção de um ambiente constante e preferido, seja manual ou automático.

Um exemplo simples poderia ser o controle da temperatura em uma sala. Controle manual significa a presença de uma pessoa em um local que verifica as condições presentes (sensor), compara com o valor desejado (processamento) e toma as medidas adequadas para obter o valor desejado (atuador). O problema com este método é que não é muito confiável, pois uma pessoa está sujeita a erros ou negligência em seu trabalho. Além disso, outro problema é que a taxa do processo iniciado pelo atuador nem sempre é uniforme, o que significa que às vezes pode ocorrer mais rápido do que o necessário ou às vezes pode ser lento. A solução para este problema foi usar um microcontrolador para controlar o sistema. O microcontrolador é

programado para controlar o processo, de acordo com as especificações dadas, conectado em um circuito (a ser discutido posteriormente), alimentado com o valor ou condições desejadas e, assim, controla o processo para manter o valor desejado. A vantagem deste processo é que nenhuma intervenção humana é necessária neste processo. Além disso, a taxa do processo é uniforme

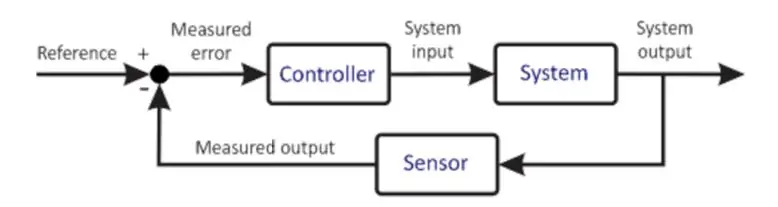
Sistema de Controle Básico

O diagrama anterior mostra uma versão muito simplificada de um Sistema de Controle. O microcontrolador é o coração de qualquer Sistema de Controle. É um componente muito importante, portanto, sua escolha de seleção deve ser feita cuidadosamente com base nos requisitos do Sistema. O microcontrolador recebe uma entrada do usuário. Esta entrada define a condição desejada do sistema. O microcontrolador também recebe uma entrada de feedback do sensor. Este sensor é conectado à saída do Sistema, cujas informações são retornadas à entrada. O microprocessador, com base em sua programação, realiza vários cálculos e fornece uma saída para o atuador. O atuador, com base na saída, controla a planta para tentar manter essas condições. Um exemplo poderia ser um acionador de motor acionando um motor onde o acionador do motor é o atuador e o motor é a planta. O motor, portanto, gira em uma determinada velocidade. O sensor conectado lê a condição da planta no momento e a realimenta para o microcontrolador. O microcontrolador novamente compara, faz cálculos e, assim, o ciclo se repete. Este processo é repetitivo e infinito, pelo qual o microcontrolador mantém as condições desejadas

Etapa 2: Sistema de controle baseado em PID

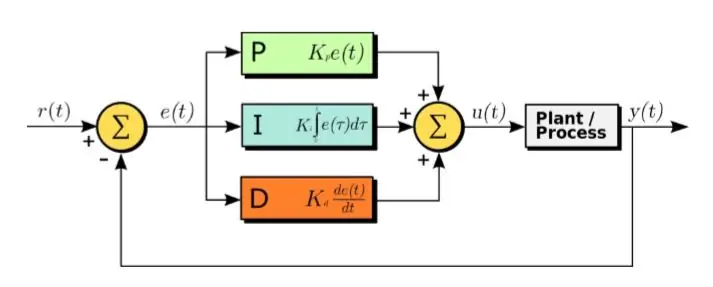
O Algoritmo PID é um método e fi ciente para projetar um Sistema de Controle.

Definição

PID significa Proporcional, Integral e Derivativo. Nesse algoritmo, o sinal de erro recebido é a entrada. E a seguinte equação é aplicada ao sinal de erro

U (t) = Kp ∗ e (t) + Kd ∗ d / dt (e (t)) + Ki ∗ integral (e (t)) (1,1)

Breve explicação

Como pode ser visto na equação acima, a integral e a derivada dos sinais de erro são calculadas, multiplicadas com suas respectivas constantes e somadas junto com a constante Kp multiplicada por e (t). A saída é então enviada para o atuador que faz o sistema funcionar. Agora vamos examinar cada parte da função por vez. Esta função afeta diretamente o tempo de subida, o tempo de queda, o pico durante o disparo, o tempo de estabilização e o erro de estado estacionário.

• Parte proporcional: A parte proporcional reduz o tempo de subida e diminui o erro de regime permanente. Isso significa que o sistema levará menos tempo para atingir seu valor de pico e quando atingir seu estado estacionário, o erro de estado estacionário será baixo. No entanto, aumenta a ultrapassagem de pico.

• Parte derivada: A parte derivada reduz o overshoot e o tempo de acomodação. Isso significa que o estado transitório do sistema será mais amortecido. Além disso, o sistema atingirá seu estado estacionário em menos tempo. No entanto, ele não tem nenhum efeito no tempo de subida ou no erro de estado estacionário.

• Parte integral: A parte integral reduz o tempo de subida e elimina completamente o erro de regime permanente. No entanto, aumenta a ultrapassagem de pico e o tempo de acomodação.

• Ajuste: Um bom sistema de controle terá baixo tempo de subida, tempo de acomodação, ultrapassagem de pico e erro de estado estacionário. Portanto, Kp, Kd, Ki precisam ser afinados para ajustar a contribuição dos fatores acima, a fim de adquirir um bom Sistema de Controle.

A figura foi anexada mostrando o efeito da alteração de vários parâmetros no algoritmo PID.

Etapa 3: Robô de autoequilíbrio

Um robô com equilíbrio automático é um robô de duas rodas com várias camadas.

O robô tentará se equilibrar com a aplicação de quaisquer forças desiguais. Ele se equilibrará pela aplicação de força opondo-se à resultante das forças no robô.

Métodos de auto-equilíbrio

Existem quatro métodos de autoequilíbrio de robôs. São os seguintes:

Auto-equilíbrio usando dois sensores de inclinação IR

Esta é uma das formas mais cruéis de equilibrar o robô, pois requer muito menos hardware e um algoritmo relativamente fácil. Nesta abordagem, dois sensores IR inclinados são usados para medir a distância entre o solo e o robô. Com base na distância calculada, o PID pode ser usado para acionar os motores para equilibrar o robô de acordo. Uma desvantagem deste método é que o sensor IR pode perder algumas leituras. Outro problema é que uma interrupção e loops são necessários para o cálculo da distância, o que aumenta a complexidade de tempo do algoritmo. Conseqüentemente, este método de balancear o robô não é muito e fi ciente.

Autoequilíbrio usando acelerômetro

O acelerômetro nos dá a aceleração do corpo em 3 eixos. A aceleração orientada no eixo y (para cima) e no eixo x (para frente) nos dá a medida para calcular a direção da gravidade e, portanto, calcular o ângulo de inclinação. O ângulo é calculado da seguinte forma:

θ = arctan (Ay / Ax) (1,2)

A desvantagem de usar este método é que durante o movimento do robô, a aceleração horizontal também será adicionada às leituras, que é um ruído de alta frequência. Conseqüentemente, o ângulo de inclinação será impreciso.

Auto-equilíbrio usando giroscópio

Um giroscópio é usado para calcular as velocidades angulares ao longo dos três eixos. O ângulo de inclinação é obtido usando a seguinte equação.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1,3)

Uma grande desvantagem de usar o giroscópio é que ele tem um pequeno DC Bias, que é um ruído de baixa frequência e em pouco tempo os valores retornados estão completamente errados. Isso, após a integração, fará com que o ponto zero se afaste. Como resultado, o robô permanecerá em sua posição vertical por algum tempo e cairá assim que chegar a deriva.

Auto-equilíbrio usando acelerômetro e giroscópio

Como discutido acima, usar apenas acelerômetro ou giroscópio não nos dará o ângulo correto de inclinação. Para dar conta disso, tanto o acelerômetro quanto o giroscópio são usados. Ambos estão integrados no MPU6050. Nesse caso, obtemos os dados de ambos e depois os fundimos usando o Filtro de Kalman ou o Filtro Complementar.

• Filtro de Kalman: O filtro de Kalman calcula a melhor estimativa do estado de um sistema dinâmico a partir de medições ruidosas, minimizando o erro quadrático médio da estimativa. Opera em duas etapas, previsão e correção, dadas as equações estocásticas discretas que descrevem a dinâmica do sistema. No entanto, é um algoritmo muito complexo de implementar, especialmente em um hardware limitado de um microcontrolador.

• Filtro complementar: este algoritmo usa principalmente os dados obtidos do giroscópio e os integra ao longo do tempo para obter o ângulo de inclinação. Ele também usa uma pequena proporção de leituras do acelerômetro. O filtro complementar, de fato, minimiza o ruído de alta frequência do acelerômetro e o ruído de baixa frequência do giroscópio e, em seguida, os funde para fornecer o melhor ângulo preciso de inclinação.

Etapa 4: Projeto do robô

Projetamos um robô de autoequilíbrio usando controlador derivativo proporcional implementado pelo filtro complementar para MPU6050. Este pequeno modelo de Auto Balanceamento de Robô nos ilustrará a utilidade de Sistemas de Controle no Auto Balanceamento de Robôs.

Implementação de sistema:

O sistema é um robô que se equilibra automaticamente. Ele é implementado usando o Controlador PID, que é um Controlador Derivativo Integral Proporcional. Equilibramos o robô dirigindo suas rodas na direção de sua queda. Ao fazer isso, estamos tentando manter o centro de gravidade do robô acima do ponto de pivô. Para mover as rodas na direção de sua queda, devemos saber onde o robô está caindo e a velocidade em que está caindo. Esses dados são obtidos usando o MPU6050, que possui um acelerômetro e um giroscópio. MPU6050 mede o ângulo de inclinação e dá sua saída para o Microcontrolador. O MPU6050 tem interface com a placa STM por meio de I2C. Em I2C, um fio é para o relógio, que é denominado SCL. O outro é para a transferência de dados que é SDA. Nesse caso, é utilizada a comunicação mestre-escravo. O endereço inicial e o endereço final são especificados para saber de onde os dados estão começando e onde estão terminando. Implementamos o Filtro Complementar aqui para MPU6050, que é um filtro matemático para mesclar as saídas do acelerômetro e do giroscópio. Após obter os dados do MPU6050, o microcontrolador fará cálculos para saber onde ele está caindo. Com base nos cálculos, o microcontrolador STM dará comandos ao motorista do motor para conduzir os veículos na direção da queda, o que equilibrará o robô.

Etapa 5: Componentes do projeto

Os seguintes componentes foram usados no projeto do robô de autoequilíbrio:

STM32F407

Um microcontrolador projetado pela ST Microelectronics. Ele funciona na arquitetura ARM Cortex-M.

Motorista L298N

Este IC é usado para acionar o motor. Recebe duas entradas externas. Um do microcontrolador que fornece um sinal PWM. Ajustando a largura do pulso, a velocidade do motor pode ser ajustada. Sua segunda entrada é a fonte de tensão necessária para acionar o motor que é uma bateria de 12 V no nosso caso.

Motor DC

Um motor DC funciona com alimentação DC. Neste experimento, o Motor DC está funcionando usando os optoacopladores conectados ao driver do motor. Para acionar o motor, usamos o Motor Drive L298N.

MPU6050

MPU6050 é usado para obter informações sobre onde o robô está caindo. Ele mede o ângulo de inclinação em relação ao ponto de inclinação zero que é a posição do MPU6050 quando o programa começa a funcionar.

O MPU6050 possui um acelerômetro de 3 eixos e um giroscópio de 3 eixos. O acelerômetro mede a aceleração ao longo dos três eixos e o giroscópio mede a taxa angular em torno dos três eixos. Para combinar a saída, devemos filtrar os ruídos de ambos. Para filtrar os ruídos, temos o filtro Kalman e Complementary. Implementamos filtro complementar em nosso projeto.

Casal Opto 4N35

Um optoacoplador é um dispositivo usado para isolar a parte de baixa tensão e a parte de alta tensão do circuito. Como o nome sugere, ele funciona com base na luz. Quando a parte de baixa tensão recebe um sinal, a corrente flui na parte de alta tensão

Etapa 6: Estrutura do Robô

A estrutura do robô é explicada da seguinte forma:

Estrutura Física

O robô com autobalanceamento consiste em duas camadas feitas de vidro plástico transparente. Os detalhes das duas camadas são fornecidos abaixo:

Primeira Camada

Na parte inferior da primeira camada, colocamos uma célula para alimentar a placa STM. Além disso, dois motores de 4 volts cada foram colocados em cada lado com pneus conectados para o robô se mover. Na parte superior da primeira camada, foram colocadas duas baterias de 4 volts cada (8 volts no total) e o acionador do motor IC (L298N) para a operação dos motores.

Segunda Camada

Na camada superior do robô, colocamos a placa STM na placa Perf. Outra placa de perf de 4 opto-acopladores é colocada na camada superior. O giroscópio também é colocado na camada superior do robô do lado inferior. Ambos os componentes são colocados na parte central para que o centro de gravidade seja mantido o mais baixo possível.

Centro de Gravidade do Robô

O centro de gravidade é mantido o mais baixo possível. Para isso, colocamos baterias pesadas na camada inferior e componentes leves como placa STM e optoacopladores na camada superior.

Etapa 7: Código

O código foi compilado no Atollic TrueStudio. STM studio foi usado para fins de depuração.

Etapa 8: Conclusão

Depois de muita experimentação e observação, finalmente chegamos ao ponto em que resumimos nossos resultados e discutimos até que ponto conseguimos implementar e trabalhar a eficácia do sistema.

Revisão Geral

Durante a experimentação, a velocidade do motor foi controlada com sucesso usando o Algoritmo PID. A curva, entretanto, não é exatamente uma linha reta suave. Existem muitas razões para isso:

• O sensor, embora conectado a um filtro passa-baixo, ainda fornece certos debouncings finitos; estes são devido às resistências não lineares e alguns motivos inevitáveis da eletrônica analógica.

• O motor não gira suavemente sob baixa tensão ou PWM. Ele fornece empurrões que podem causar alguns valores errados no sistema.

• Devido à oscilação, o sensor pode perder algumas fendas que fornecem valores mais altos. • Outra razão importante para erros pode ser a frequência do clock central do microcontrolador STM. Este modelo de microcontrolador STM fornece um clock central de 168MHz. Embora este problema tenha sido tratado neste projeto, existe uma noção geral sobre este modelo de que ele não fornece exatamente essa alta frequência.

A velocidade de malha aberta fornece uma linha muito suave com apenas alguns valores inesperados. O Algoritmo PID também está funcionando bem, proporcionando um tempo de estabilização muito baixo do motor. O Algoritmo PID do motor foi testado em várias tensões mantendo a velocidade de referência constante. A mudança de tensão não altera a velocidade do motor, mostrando que o Algoritmo PID está funcionando bem

Eficácia

Aqui, discutimos a eficácia do controlador PID que observamos durante a experimentação.

Implementação Simples

Vimos na seção de experimentação e observações que um controlador PID é muito fácil de implementar. Requer apenas três parâmetros ou constantes que devem ser definidos para ter um sistema de controle de velocidade

Eficiência incomparável para sistemas lineares

O controlador PID linear é o mais e fi ciente na família de controladores porque a lógica é muito simples e a aplicação é difundida no caso de aplicações lineares ou razoavelmente lineares.

Limitações

Explicamos de forma abstrata sobre as limitações deste sistema. Aqui, discutimos alguns deles que observamos.

Seleção de constantes

Vimos que, embora um controlador PID seja fácil de implementar, ainda é uma grande desvantagem do sistema que a etapa de selecionar o valor das constantes seja trabalhosa; pois é preciso fazer cálculos difíceis. A outra forma é o método de acerto e teste, mas também não é e fi ciente.

Constantes nem sempre constantes

Os resultados experimentais mostraram que para diferentes valores da velocidade de referência do motor, o controlador PID apresentou mau funcionamento para os mesmos valores das constantes PID. Para velocidades diferentes, as constantes tiveram que ser selecionadas de forma diferente e isso aumenta o custo computacional exponencialmente.

Não Linear

O controlador PID utilizado em nosso caso é linear, portanto, pode ser aplicado apenas a sistemas lineares. Para sistemas não lineares, o controlador deve ser implementado de forma diferente. Embora diferentes métodos não lineares de PID estejam disponíveis, eles requerem a seleção de mais parâmetros. Isso novamente torna o sistema indesejável devido ao alto custo computacional.

Impulso inicial necessário

Mostramos na seção de experimentação que para uma velocidade de referência razoavelmente pequena onde o erro é bastante pequeno na partida, o PWM fornecido pelo PID é tão pequeno que não gera o torque de partida necessário para o motor. Portanto, o motor em alguns testes não funciona ou em outros fornece um grande overshoot e um tempo de estabilização mais longo.

Etapa 9: Agradecimentos especiais

Agradecimentos especiais aos membros do meu grupo que me ajudaram neste projeto.

Vou enviar o link para o vídeo em breve.

Espero que você ache este instrutível interessante.

Aqui é Tahir Ul Haq do UET assinando. Saúde !!!