
Índice:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 11:39.
- Última modificação 2025-01-23 15:03.

Se você tiver tempo para assistir ao vídeo acima, notará que há alguns ruídos estranhos causados pelos motores da direção, parando de vez em quando enquanto o WEEDINATOR faz uma curva de 3 pontos. Os motores estão essencialmente colidindo uns com os outros, pois o raio de giro é diferente de dentro para fora e a distância que a roda percorre é diferente por grau de giro.
A geometria da curva pode ser trabalhada esboçando 8 ou mais permutações da curva, dando exemplos de curvas em ângulos diferentes na roda interna de 0 (sem curva) a 90 (travamento total) graus. Parece complicado?
A maioria dos pequenos robôs com rodas não tenta ter nenhum tipo de direção sofisticada e confia, de forma muito eficaz, simplesmente na mudança da velocidade relativa dos motores em cada lado do veículo, que é praticamente a mesma de uma escavadeira ou tanque com esteiras trabalho. Isso é ótimo se você estiver avançando sobre uma zona de guerra cheia de crateras, atirando em tudo que se move, mas em um ambiente agrícola tranquilo é importante causar o mínimo possível de danos ao solo e ao solo, para que as rodas para frente e para trás sejam não apropriado!
A maioria dos carros e tratores tem um dispositivo muito útil chamado 'Diferencial', exceto os carros que você vê em filmes americanos antigos, onde você pode ouvir os pneus cantando loucamente toda vez que eles dobram uma esquina. Os americanos ainda constroem carros assim? Com o WEEDINATOR, podemos programar o diferencial nos motores de acionamento calculando a fórmula para as velocidades e ângulos relativos das rodas em qualquer ângulo de giro específico. Ainda parece complicado?
Aqui está um exemplo rápido:
Se o WEEDINATOR está fazendo uma curva e tem a roda interna a 45 graus, a roda externa NÃO está a 45 graus, é mais como 30 graus. Além disso, a roda interna pode estar girando a 1 km / hora, mas a roda externa será significativamente mais rápida, cerca de 1,35 km / hora.
Etapa 1: configuração da geometria
Algumas suposições básicas são feitas para começar:
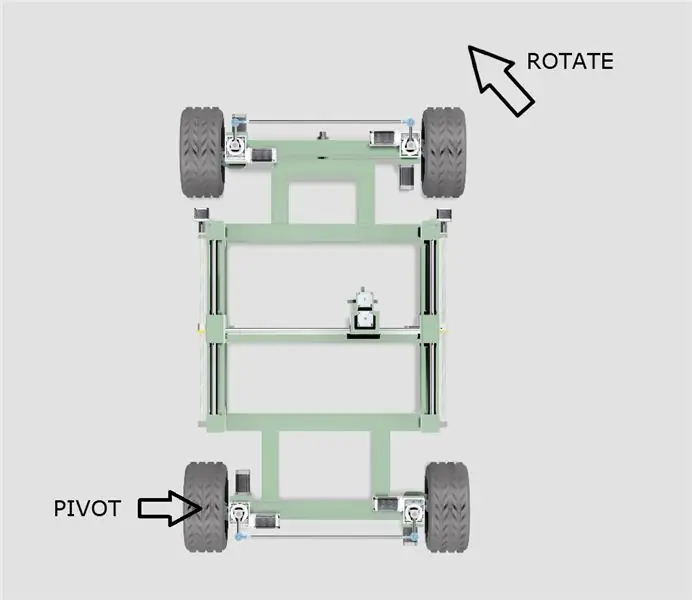
- O chassi girará em torno de uma das rodas traseiras, conforme mostrado no diagrama acima.
- O centro efetivo do círculo pivô se moverá ao longo de uma linha estendida a partir do centro das duas rodas traseiras, dependendo do ângulo da curva.
- A geometria assumirá a forma de uma curva sinusoidal.
Etapa 2: desenhos em escala dos ângulos e raios das rodas

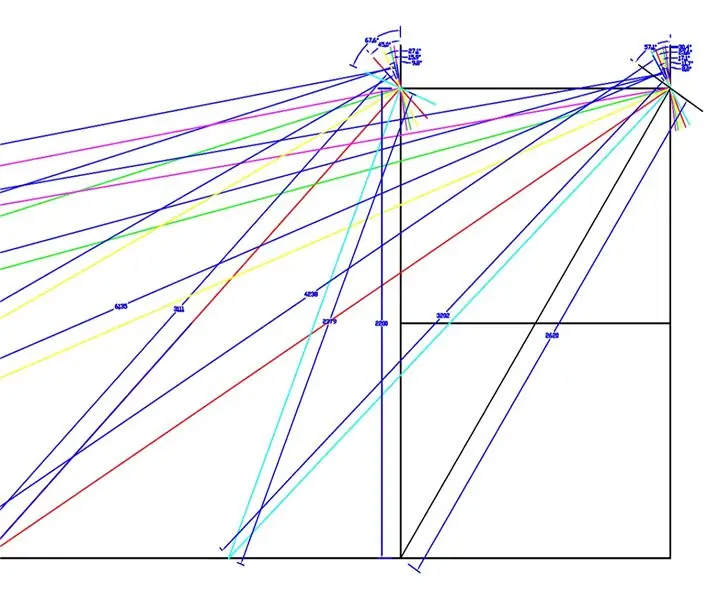
Um desenho em escala real foi feito das rodas dianteiras e do chassi do WEEDINATOR com 8 permutações diferentes do ângulo interno da roda entre 0 e 90 graus e os respectivos centros de giro foram mapeados conforme mostrado nos desenhos acima.
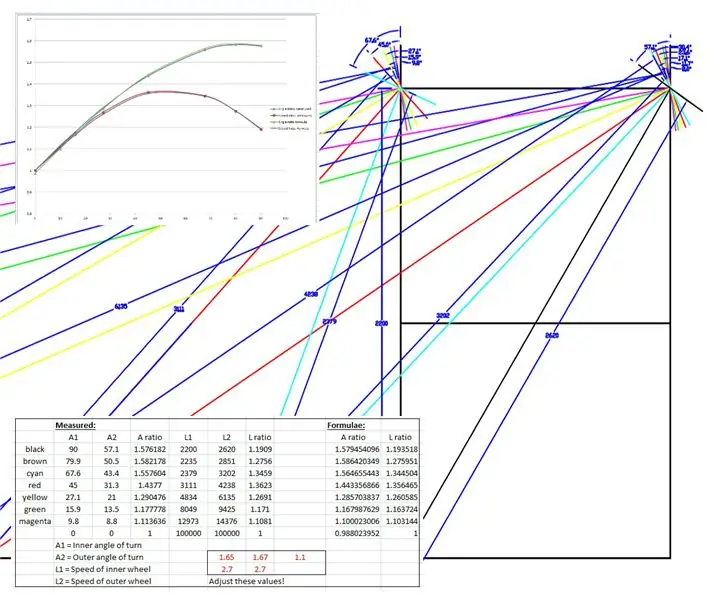
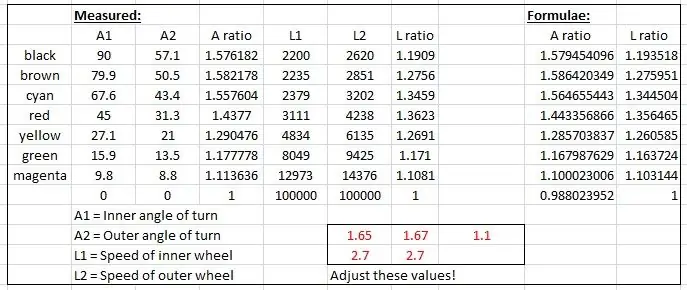
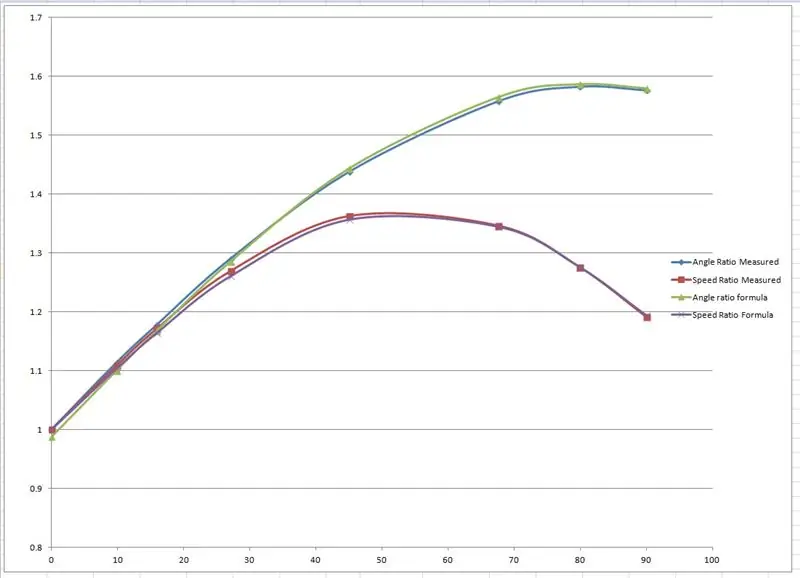
Os raios efetivos foram medidos a partir do desenho e plotados em um gráfico no Microsoft Excel.
Dois gráficos foram produzidos, um da proporção dos eixos das rodas dianteiras direito e esquerdo e outro para a proporção dos dois raios para cada ângulo de giro específico.
Em seguida, "falsifiquei" algumas fórmulas para imitar os resultados empíricos com base em uma curva sinusoidal. Um dos fudgings tem a seguinte aparência:
speedRatio = (sin (interno * 1,65 * pi / 180) +2,7) / 2,7; // interno é o ângulo de giro interno.
As curvas foram alteradas alterando os valores mostrados em vermelho no arquivo Excel até que as curvas se ajustassem.
Etapa 3: Codificando as Fórmulas
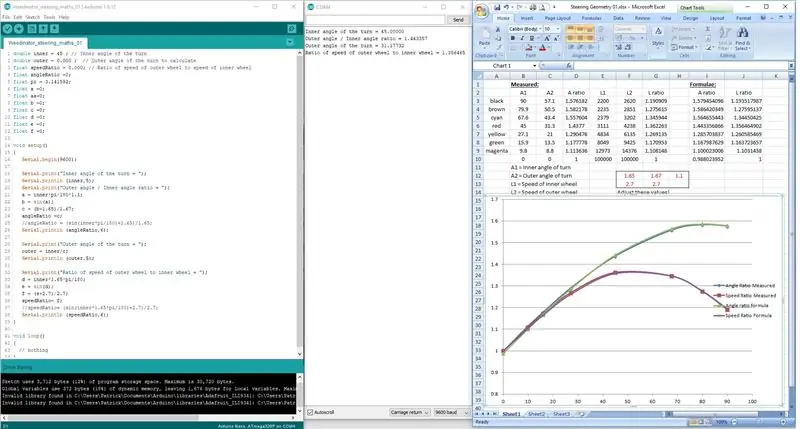
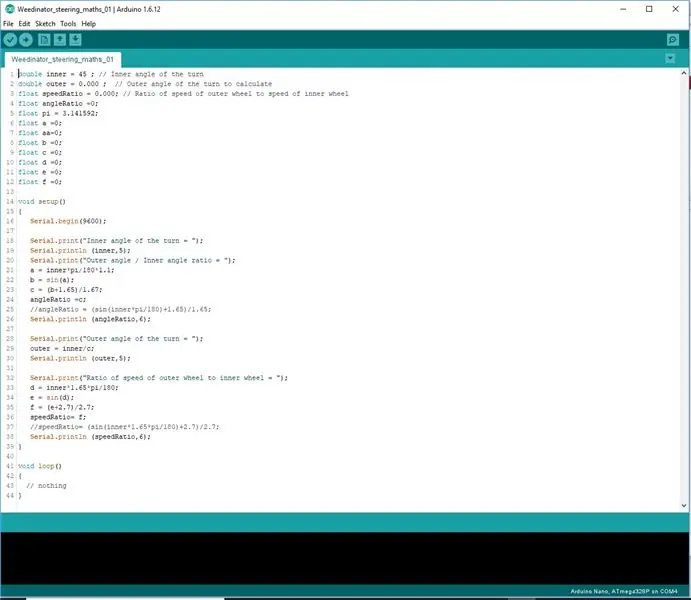
Em vez de tentar codificar as fórmulas em uma linha, elas foram divididas em 3 estágios para permitir que o Arduino processe a matemática corretamente.
Os resultados são mostrados no display da porta serial e verificados com os resultados medidos no desenho da escala.
Recomendado:
Tutorial do aplicativo IoT Kraken Jr. Parte 2 - Capturando Cid e código de autenticação: 4 etapas

Kraken Jr. IoT App Tutorial Parte 2 - Capturando Cid e Código Auth: Tutorial Parte 1 (Registro de Email e Ativação) Tutorial Parte 2 (Capturando Cid e Código de Auth) Tutorial Parte 3 (Arduino Registration) Registrando um novo Controlador em seu Kraken Jr. O aplicativo é fácil. No entanto, serão necessários alguns passos para cumprir
Arduino Hot Wheels Speed Track Parte 2 - Código: 5 etapas

Arduino Hot Wheels Speed Track Parte # 2 - Código: Na primeira parte deste projeto, construímos o hardware para o protótipo em 2 breadboards. E nesta parte iremos repassar o código, como ele funciona e, em seguida, testá-lo. Certifique-se de assistir ao vídeo acima para toda a revisão do código e demonstração do
Robot De Tracción Diferencial (Unidade Diferencial): 10 Passos

Robot De Tracción Diferencial (Unidade Diferencial): La rob ó tica de enjambre se inspira en insetos que agem ú an colaborativamente. É uma disciplina basada em conjuntos de robôs que são coordenados para realizar tareas grupales. Os robôs individuais deben ser capaces de sensar y actuar e
☠WEEDINATOR☠ Parte 3: Construção do chassi: 8 etapas (com imagens)

☠WEEDINATOR☠ Parte 3: Construção do chassi: O inverno é a época perfeita para construir máquinas, especialmente quando a soldagem e o corte a plasma estão envolvidos, pois ambos fornecem uma boa quantidade de calor. Se você está se perguntando o que é um cortador de plasma, continue lendo para procedimentos detalhados
☠WEEDINATOR☠ Parte 2: Navegação por satélite: 7 etapas (com imagens)

☠WEEDINATOR☠ Parte 2: Navegação por satélite: Nasce o sistema de navegação Weedinator! Um robô agrícola itinerante que pode ser controlado por um telefone inteligente … E em vez de apenas passar pelo processo normal de como ele é montado, pensei em tentar explicar como ele realmente funciona - obviamente
